Consider a continuous Markov chain with two states S = {0, 1}. Assume the holding time parameters are given by 0 = 1

Consider a continuous Markov chain with two states S = {0, 1}. Assume the holding time parameters are given by λ₀ = λ₁ = λ > 0. That is, the time that the chain spends in each state before going to the other state has an Exponential(λ) distribution.

a. Draw the state diagram of the embedded (jump) chain.

b. Find the transition matrix P(t). You might want to use the following identities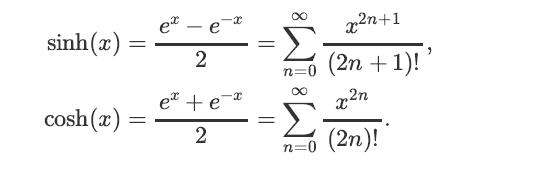

sinh(2) cosh (x) = = et - e 2 e +ex 2 = = xn+1 n=0 (2n +1)!' 2n x n=0 (2n)!