Consider two random variables X and Y with the same range RX = RY = {a1, a2, a3}, and suppose that E(X) = E(Y) and Var(X) = Var(Y).

(i) Prove that E(X2) = E(Y2).

(ii) Show that the quantities xi = P(X = ai) − P(Y = ai), i = 1, 2, 3, satisfy a homogeneous linear system of equations, for which the determinant of the coefficient matrix for the unknowns has the form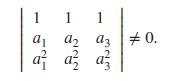

(iii) Explain why the distributions of the random variables X and Y coincide, i.e.
we have P(X = ai) = P(Y = ai)
for i = 1, 2, 3.

1 1 1 aaa3 a aa # 0.