Given the following data from a randomized block design, (a) Decompose each observation (y_{i j}) as [begin{aligned} y_{i j}= & bar{y}_{bullet}+left(bar{y}_{bullet bullet}-bar{y}_{bullet bullet} ight)+left(bar{y}_{bullet j}-bar{y}_{bullet

Given the following data from a randomized block design,

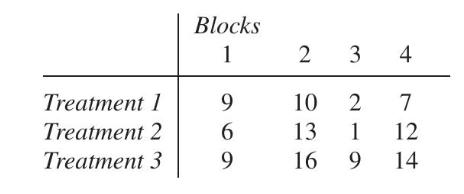
(a) Decompose each observation \(y_{i j}\) as \[\begin{aligned} y_{i j}= & \bar{y}_{\bullet}+\left(\bar{y}_{\bullet \bullet}-\bar{y}_{\bullet \bullet}\right)+\left(\bar{y}_{\bullet j}-\bar{y}_{\bullet \bullet}\right) \\ & +\left(y_{i j}-\bar{y}_{i \bullet}-\bar{y}_{\bullet j}+\bar{y}_{\bullet \bullet}\right) \end{aligned}\]

(b) Obtain the sums of squares and degrees of freedom for each array.

(c) Construct the analysis of variance table and test for differences among the treatments with \(\alpha=\) 0.05 .

Blocks 1 2 3 4 Treatment 1 9 10 2 7 Treatment 2 6 13 1 12 Treatment 3 9 16 9 14