In some applications, we need to work with complexvalued random processes. More specifically, a complex random process X(t) can be written as X(t) = X_r(t) +jX_i(t), where X_r(t) and X_i(t) are two real-valued random processes and j = √−1. We define the mean function and the autocorrelation function as

Let X(t) be a complex-valued random process defined as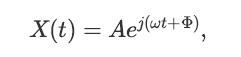

where Φ ∼ Uniform(0, 2π), and A is a random variable independent of Φ with EA = μ and Var(A) = σ².

a. Find the mean function of X(t), μ_X(t).

b. Find the autocorrelation function of X(t), R_X(t₁, t₂).

x(t) = E[X(t)] = E[X, (t)] + jE[Xi(t)] = x, (t) + jux, (t); Rx (t1, t2) E[X(t)X* (t)] = = E [(Xr(t) + jXi(t1)) (Xr (t2) jXi(t2))].