Let {X(t), t R} be a continuous-time random process. The time average mean of X(t) is

Question:

Let {X(t), t ∈ R} be a continuous-time random process. The time average mean of X(t) is defined as (assuming that the limit exists in mean-square sense)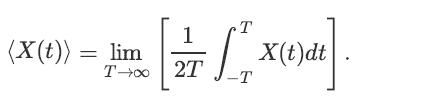 (X(t)) = lim T [ 1 2T T -T X(t)dt

Consider the random process {X(t), t ∈ R} defined as

where U ∼ Uniform(0, 2π). Find ⟨X(t)⟩.

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Introduction To Probability Statistics And Random Processes

ISBN: 9780990637202

1st Edition

Authors: Hossein Pishro-Nik

See More Books

Question Posted: Nov 01, 2023 01:41 PM

See More Questions

Let I := [a, b and let f : I R be a continuous function such that f(x) > 0 for each x in I. Prove that there exists a number a > 0 such that f(x) > a for all x I.
Write a MARIE program to encode your name and ID as a string The following example of a MARIE string "nameID" encodes a name and an ID using ASCII characters. The "name" is separated from the ID by...
Let I := [a, b] and let f : I R be a continuous function on I such that for each x in I there exists y in I such that | f (y)| < | f(x)|. Prove there exists a point c in I such that f(c) = 0.
Prepare a statement of cash flows in proper form using the inflows and outflows from questions 4-15. Assume net income (earnings after taxes) from the 2018 income statement was $10,628, and $5,000 in...
Croftmark Co. began operations on May 1, 2010. Its Work in Process Inventory account on May 31 appeared as follows: The company applies overhead on the basis of direct labor cost. Only one job was...
Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. Different parametrizations of the same curve...
A liquid (viscosity $=0.002 \mathrm{~N} \cdot \mathrm{s} / \mathrm{m}^{2}$; density $=1000 \mathrm{~kg} / \mathrm{m}^{3}$ ) is forced through the circular tube shown in Fig. P6.93. A differential...
Three linked bungee jumpers are depicted in Fig. P25.26. If the bungee cords are idealized as linear springs (i.e., governed by Hooke's law), the following differential equations based on force...
We have a non-rotating space station in the shape of a long thin uniform rod of mass 4.45 x 10^6 kg and length 1387 meters. Small probes of mass 9598 kg are periodically launched in pairs from two...
Let X(t) be a zero-mean Gaussian random process with R X () = 8 sinc(4). Suppose that X(t) is input to an LTI system with transfer function If Y (t) is the output, find P(Y (2) H(f) = 2 0 |f| <1...
In some applications, we need to work with complexvalued random processes. More specifically, a complex random process X(t) can be written as X(t) = X r (t) +jX i (t), where X r (t) and X i (t) are...
According to the American Pet Products Manufacturers Associations 20172018 National Pet Owners Survey, there is a 38% probability that a U.S. household owns a cat. If a U.S. household is randomly...
Which simple scheduling concept can be applied to help schedule workers for a service operation with changing staffing requirements throughout the day?
What is the official definition of a recession?
What is the key difference between real business cycle models and other business cycle models?
In each of the following, name the term defined or answer the question. Answers are listed at the bottom. 1. This is the currently used term for a system that schedules, dispatches, tracks, monitors,...
What is the role of unanticipated price changes in the new classical model of business cycles?
The U.S. Golf Association is considering a ban on long and belly putters. This has caused a great deal of controversy among both amateur golfers and members of the Professional Golf Association (PGA)...
Suppose the concentration of glucose inside a cell is 0.1 mm and the cell is suspended in a glucose solution of 0.01 mm. a. What would be the free energy change involved in transporting 10-o mole of...
As a library or internet assignment, find the U.S. productivity rate (increase) last year for the (a) national economy, (b) manufacturing sector, (c) service sector.
Solutions Corporation, a computer vendor and consulting company, uses the accrual method of accounting. Its tax year is the calendar year. The following are three of the corporations transactions...
Pamello, Inc., an engineering consulting firm, uses the cash method of accounting and is a calendar year taxpayer. Compute the amount of Pamellos current year deductions for the following...
KINGBIRD INC. Statement of Retained Earnings Year Ended July 31, 2024 Retained Earnings, August 1, 2023 Add Profit/(Loss) for the Year Less Cash Dividends $ 366,080 $ Retained Earnings, July 31, 2024...
Hard Hat Company is in the process of purchasing several large pieces of equipment from Machine Corporation. Several financing alternatives have been offered by Machine: 1. Pay $1,120,000 in cash...
Although workplace discrimination is illegal and laws against it are enforced by several agencies, including the U.S. Equal Employment Opportunity Commission, it still occurs. Workplace...

Let {X(t), t R} be a continuous-time random process. The time average mean of X(t) is

Question:

(X(t)) = lim T→∞ [ 1 2T T -T X(t)dt

Step by Step Answer:

The time average mean of a continuoustime random process Xt t R is defined as follows Equation 1 Xt ...View the full answer

Introduction To Probability Statistics And Random Processes

Students also viewed these Business questions