In this problem, our goal is to complete the proof of the equivalence of the first and the second definitions of the Poisson process. More specifically, suppose that the counting process {N(t), t ∈ [0,∞)} satisfies all the following conditions:

1. N(0) = 0.

2. N(t) has independent and stationary increments.

3. We have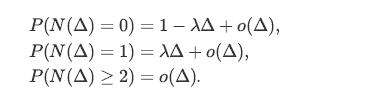

We would like to show that N(t) ∼ Poisson(λt). To this, for any k ∈ {0, 1, 2,⋯}, define the function g_k(t) = P(N(t) = k).

a. Show that for any Δ > 0, we have

b. Using Part (a), show that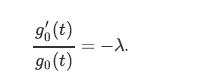

c. By solving the above differential equation and using the fact that g₀(0) = 1, conclude that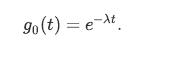

d. For k ≥ 1, show that

e. Using the previous part show that

which is equivalent to

f. Check that the function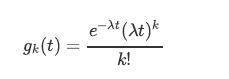

satisfies the above differential equation for any k ≥ 1. In fact, this is the only solution that satisfies g₀(t) = e^−λt, and g_k(0) = 0 for k ≥ 1.

P(N(A) = P(N(A) 1) = A + 0(A), P(N(A) 2) = o(A). = 0) = 1 ->A + o(A),