In this problem, we would like to show that the geometric random variable is memoryless. Let X ∼ Geometric(p). Show that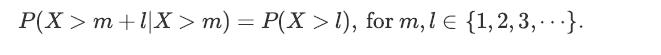

We can interpret this in the following way: Remember that a geometric random variable can be obtained by tossing a coin repeatedly until observing the first heads. If we toss the coin several times, and do not observe a heads, from now on it is like we start all over again. In other words, the failed coin tosses do not impact the distribution of waiting time from this point forward. The reason for this is that the coin tosses are independent.

P(X > m +1|X > m) = P(X > 1), for m, l {1,2,3,...}.