Instead of using the computing formula on page 367, we can obtain the correlation coefficient \(r\) with the formula

\[r= \pm \sqrt{1-\frac{\sum(y-\widehat{y})^{2}}{\sum(y-\bar{y})^{2}}}\]

which is analogous to the formula used to define \(ho\). Although the computations required by the use of this formula are tedious, the formula has the advantage that it can be used also to measure the strength of nonlinear relationships or relationships in several variables. For instance, in the multiple linear regression in Example 12, one could calculate the predicted values by means of the equation

\[\widehat{y}=46.4+7.78 x_{1}-1.65 x_{2}\]

and then determine \(r\) as a measure of how strongly \(y\), the twists required to break one of the forged alloy bars, depends on both percentages of alloying elements present.

(a) Using the data in Example 12, find \(\sum(y-\bar{y})^{2}\)

(b) Using the regression equation obtained in Example 12, calculate \(\widehat{y}\) for the 16 points and then determine \(\sum(y-\widehat{y})^{2}\).

(c) Substitute the results obtained in (a) and (b) into the above formula for \(r\). The result is called the multiple correlation coefficient.

Data From Example 12

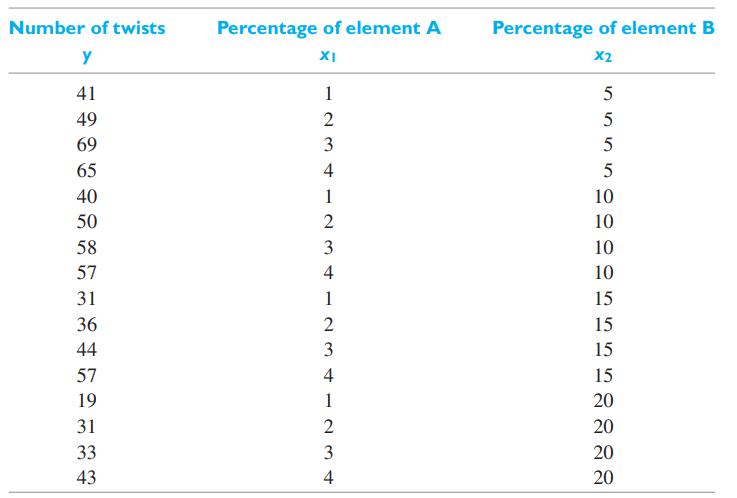
EXAMPLE 12 A multiple regression with two predictor variables The following are data on the number of twists required to break a certain kind of forged alloy bar and the percentages of two alloying elements present in the metal: