Let {N(t), t [0,)} be a Poisson process with rate . Let T 1 , T 2 , be the arrival times for

Let {N(t), t ∈ [0,∞)} be a Poisson process with rate λ. Let T₁, T₂, ⋯ be the arrival times for this process. Show that

One way to show the above result is to show that for sufficiently small Δ_i, we have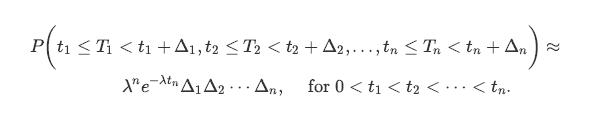

fT T2T (t1, t2, tn) = X"e-tn, ,tn)=X"e-tn, for 0