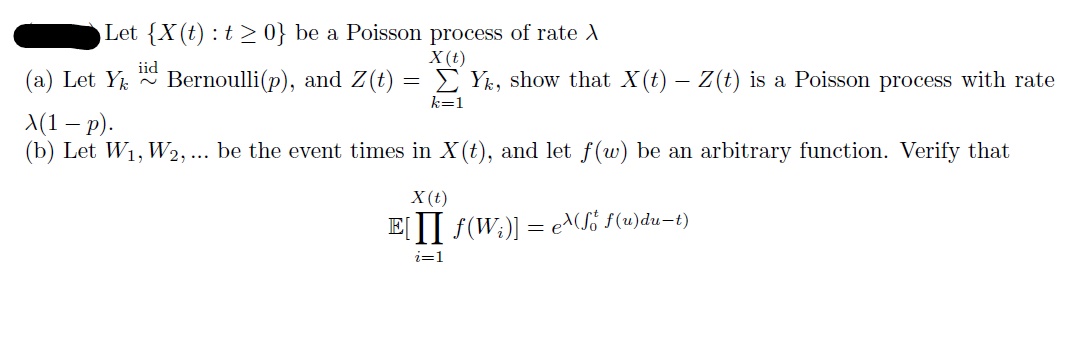
Let {X(t) : t 2 0} be a Poisson process of rate 1 X (t) (a) Let Yk ~ Bernoulli(p), and Z(t) = _ Yk, show that X(t) - Z(t) is a Poisson process with rate k=1 X(1 - p). (b) Let W1, W2, ... be the event times in X (t), and let f(w) be an arbitrary function. Verify that X (t ) E[[I f ( W.)] = ex(Sof(u)du-t) i=1