Question: Let X 1 , X 2 , X 3 , be independent random variables, where X n Bernoulli (1 n) for n =
Let X1, X2, X3, ⋯ be independent random variables, where Xn ∼ Bernoulli (1 n) for n = 2, 3,⋯. The goal here is to check whether Xn a.s.→ 0.
1. Check that
2. Show that the sequence X1, X2, . . . does not converge to 0 almost surely using Theorem 7.6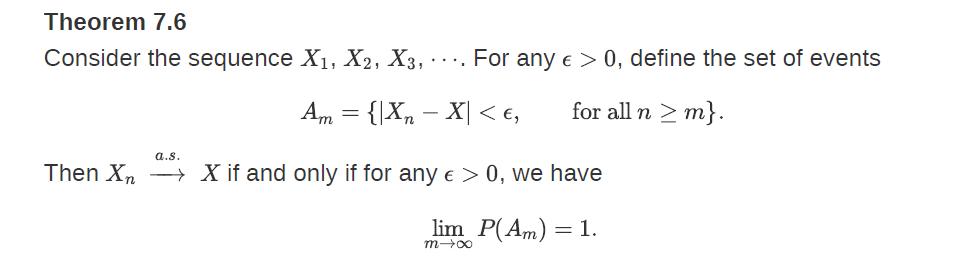
x= P(|X| > ) = . n=1
Step by Step Solution
★★★★★
3.44 Rating (173 Votes )
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock
1 We first note that for 0 1 we have 2 To use Theorem 76 we define Note that for 0 1 we hav... View full answer
Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock
Study Help