Let X(t) be a zero-mean WSS Gaussian random process with RX() = e 2 . Suppose that X(t) is input to an LTI system

Let X(t) be a zero-mean WSS Gaussian random process with RX(τ) = e^−πτ2. Suppose that X(t) is input to an LTI system with transfer function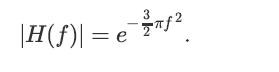

Let Y (t) be the output.

a. Find μ_Y .

b. Find R_Y (τ) and Var(Y (t)).

c. Find E[Y (3)|Y (1) = −1].

d. Find Var(Y (3)|Y (1) = −1).

e. Find P(Y (3)

|H(f)| = e