Question: Let {X(t), t R} be a WSS random process. Show that for any > 0, we have P(|X(t + r) - X(t)| >

Let {X(t), t ∈ R} be a WSS random process. Show that for any α > 0, we have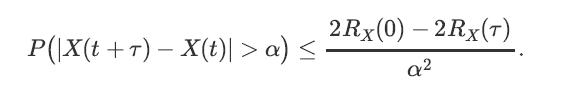P(|X(t + r) - X(t)| > a) 2Rx(0) -2RX(T) a

P(|X(t + r) - X(t)| > a) 2Rx(0) -2RX(T) a

Step by Step Solution

★★★★★

3.42 Rating (158 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

The inequality youve presented is an application of Chebyshevs inequality for random processes Le... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Introduction To Probability Statistics Questions!

Q:

Let X (t) be a WSS random process with mean uX and autocorrelation function RXX ( r ). Consider forming a new process according to a) Find the mean function of Y (t). b) Find the autocorrelation...

Q:

If one attempted to dualize the notion of free module over a ring R (and called the object so defined "co-free") the definition would read: An R-module F is co-free on a set X if there exists a...

Q:

Let {X(t), t R} be a WSS random process. Suppose that R X () = R X (0) for some > 0. Show that, for any t, we have X(t+r) = X(t), with probability one.

Q:

Let X, , = ( X, X, , . . . , X. ) be an IID random process where P[X, = 0]= P[X, = 1]=0.5. Consider random process Y, = 0.5(X, - X,_ ). (a) Find P[Y, = 0.5| Y,_=-0.5]. (b) Find P[Y = 0.5| Y,_= -0.5,...

Q:

a Let Us Try! '\\ Hello! I hope you are having a good day. Before proceeding to Lesson 1, try to read and answer the activity below rst. Let us try rst your understanding of the concept. Get 1/2...

Q:

Solve all. 5 Consider the success run chain in Example 8.2.16. Suppose that the chain has been running for a while and is currently in state 10. (a) What is the expected number of steps until the...

Q:

Hi, it's me again Thanks for helping me with the answer last time d u 1. (a) Let Y1, Y2, ..., Yn be a random sample from a Bernoulli (p) distribution (i.e. Binomial(1, p)). Show ELI K is a minimal...

Q:

Please Solve the questions in the attachment clearly. 1 (0) A risky asset has value A at time t. A probability measure R is defined so that Av is an yle R-martingale, where v is calculated using the...

Q:

4 This assignment, based on the content of Unit 4 of the Study Guide, is worth 3% of your grade. We recommend that you hand it in after you complete Unit 4. You must show all of your work in order to...

Q:

Which of the following could be quantified as a Bernoulli random variable? a) number of persons in a hospital ward with terminal diagnoses. b) weights of deliveries at a supermarket. c) square foot...

Q:

A poll of 224 home sellers found that 25.5% were trying to sell their home without a real estate agent. The margin of error for this poll was 4.8%. Find the approximate confidence level used by the...

Q:

A national bank was robbed by a man with a small strip of tape on each side of his face. An indictment was returned against David. David was then arrested, and counsel was appointed to represent him....

Q:

Carlos is part of the WAI, and helps to develop guidelines to ensure a . all webete visitors can access content on webpages b . HTML and CSS guidelines are updated c . demain fegistration and IP...

Q:

Drive to exercise initiative in social situations

Q:

2.13 Fighting the Flu Influenza is a highly conta- gious respiratory disease that strikes as many as eight million Canadians in flu season, between October and April. To get an idea of people's...

Q:

Calculate the variance and standard deviation for the five measurements in Table 2.2, which are 5, 7, 1, 2, 4. Use the computing formula for s and compare your results with those obtained using the...

Q:

2.14 You are given n = 5 measurements: 2, 1, 1, 3, 5. a. Calculate the sample mean, X. b. Calculate the sample variance, s, using the formula given by the definition. c. Find the sample standard...

Q:

Is the key to developing an effective sales force selection or training? Explain your choice. Please do not copy the same answer from coursehero

Q:

Part 3:Brainstorm and Create Ideas BSBMGT407 Apply digital solutions to work processes Additional Resources You will be provided with the following resources before you begin each Assessment Task....

Q:

Outline the tasks that a guest room attendant must perform in order to properly clean a guest room. Please use a numeric list or bullet points.