Letting X denote the random variable that is defined as the sum of two fair dice, then

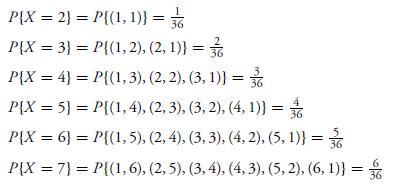
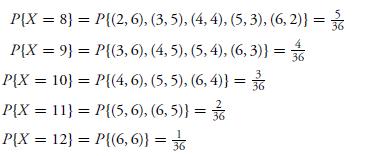
In other words, the random variable X can take on any integral value between 2 and 12 and the probability that it takes on each value is given by Equation 4.1.1. Since X must take on some value, we must have

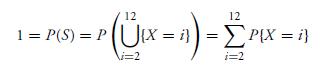
which is easily verified from Equation 4.1.1.
Another random variable of possible interest in this experiment is the value of the first die. Letting Y denote this random variable, then Y is equally likely to take on any of the values 1 through 6. That is, P{Y = i} = 1/6, i = 1, 2, 3, 4, 5, 6

P{X=2} = P{(1, 1)} = P{X=3} = P{(1, 2), (2, 1)) = P{X = 4} = P{(1, 3), (2, 2), (3, 1)} = 36 P{X=5} = P{(1, 4), (2, 3), (3, 2), (4, 1)) = P{X = 6} = P{(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)} = 36 P{X = 7} = P{(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)} = 36