Recall the birthday problem (see Example 2.12). Let 1 − pk denote the probability that in a group of k students, at least two share the same birthday. This probability is found below using Mathematica.

In[1]:= k=5;

birth= 1-Product[(366-r)/365,{r,1,k}]

birth1= N[birth]

Out[2]= 481626601/17748900625 Out[3]= 0.0271356

(Notice that, if we do not use the operator N[ ], which gives the result in decimal form, the answer is given as a fraction.) The result above was found for k = 4. If we want to plot 1 − pk, as a function of k, we have the following series of commands:

In[4]:= n=10;
birthtable= Table[{k,1-Product[(365-j+1)/365, {j,1,k}]},{k,1,n}]//N ListPlot[birthtable]
Out[5]= {{1.,0.},{2.,0.00273973},{3.,0.00820417}, {4.,0.0163559},{5.,0.0271356},{6.,0.0404625}, {7.,0.0562357},{8.,0.0743353},{9.,0.0946238}, {10.,0.116948}}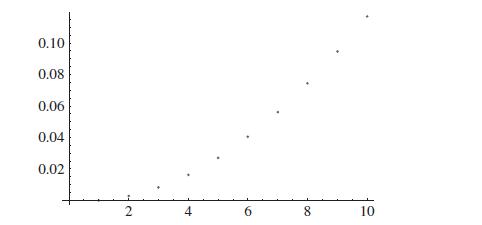

(i) Check empirically that, as k grows large, 1 − pk approaches unity.
(ii) Find the least value of k such that the corresponding probability 1 − pk is at least

(a) 50%;

(b) 90%;

(c) 95%;

(d) 99%.

0.10 0.08 0.06 0.04 0.02 2 4 8 10