Question: Consider the matrices (a) Verify that they are diagonalizable and that they commute. (b) Find the eigenvalues and eigenvectors of A and verify that its

Consider the matrices

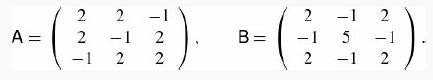
A = 2 - 1 2 - 1 2 -1 2 2

(a) Verify that they are diagonalizable and that they commute.
(b) Find the eigenvalues and eigenvectors of A and verify that its spectrum is degenerate.
(c) Are the eigenvectors that you found in part (b) also eigenvectors of B? If not, find the vectors that are simultaneous eigenvectors of both matrices.

A = 2 - 1 2 - 1 2 -1 2 2 B= 2 - 1 2 -1 2 -1 15 -1 2

Step by Step Solution

★★★★★

3.40 Rating (162 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a Since Ay A and By B the matrices are normal Equation A82 and hence diagonalizable b To get ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Introduction To Quantum Mechanics Questions!

Find all eigenvalues and eigenvectors of the following complex matrices: (a) (b) (c) (d) (o 11) 0 2 2 (1211) i-2 i+1 'I 2 + 2 2 2

Find all eigenvalues and eigenvectors of (a) The n x n zero matrix O; (b) The n x n identity matrix I.

Find the eigenvalues and eigenvectors of the matrix (a) Use the eigenvalues to compute the determinant of A. (b) Is A positive definite? Why or why not? (c) Find an orthonormal eigenvector basis of...

Please assist Consider the following. (a) Verify that A is diagonalizable by computing P AP. p-1AP = POOH (b) Use the result of part (a) and the theorem below to find the eigenvalues of A. Similar...

Consider the following. 10 -24 A = = 2 -3 4 -10 (a) Verify that A is diagonalizable by computing P-1AP. P-1AP = (b) Use the result of part (a) and the theorem below to find the eigenvalues of A....

Please, answer all of the following questions: 1. Consider the matrices O 0 1 A = 0 = 1 1 1 1 1 (1) Find a basis of the kernel and the column space of B. (2) Diagonalize B (no need of orthogonal...

ID. .LetB=( 2 1 . Consider the matrix A = (1 2). Diagonalize the matrix if possible. 1 1 0 1). Determine 32, B3, and generalize for B". 7 1 . Suppose C: (2 3 ). (a) Find the eigenvalues and their...

Problem 1: Consider the following Matrix A: A = [222] a) Find the Eigenvalues of A. Show all your work by hand b) Find the Eigenvectors of A. Show all your work by hand c) Normalize the Eigenvectors....

Math 636 Final - Quiz Component 1. The system of linear equations 2x2 x3 = 3 2x1 + x2 + 2x3 = 1 x1 + x2 + 3x3 = 2 (a) is consistent with a unique solution. (b) is consistent with infinitely many...

Find eigenvalues and eigenvectors of matrix A and determine if A is diagonalizable. Use the concepts to solve a system of linear differential equations. A. Consider a random 4 x 4 matrix A1: Create...

The Zumwalt Company is expected to pay a dividend of $2.25 per share at the end of the year, and that dividend is expected to grow at a constant rate of 5.00% per year in the future. The company's...

Suppose that two Japanese companies, Hitachi and Toshiba, are the sole producers (i.e., duopolists) of a microprocessor chip used in a number of different brands of personal computers. Assume that...

The principle of exception should be utilized fully for effective materialscontrol. Explain.

Model 8300 Telemetry system used at Wesley Long Community Hospital, Greensboro, North Carolina, is a completely self-contained, wireless, one-patient cardiac monitor.6 The system provides wireless...

In the movie Back to the Future, Doc Brown and the young Marty McFly need 1.21 GW of power for their time machine. (a) Convert that power requirement to horsepower. (b) If a stock DeLorean sports car...

A sprinter runs using a force of 200 N and a power output of 600 W. Calculate how many minutes it takes for the runner to run 1 km.

A baseball catcher stops a 98-mph fastball over a distance of 0.1 m. What is the force necessary to stop the 0.14-kg fastball?

At age 22 you invest $1,500 that earns 9 percent each year. At age 37 you invest $1,500 that earns 12 percent per year. n which case would you have more money at age 65? O investing at age 37 O...

The Corrado Miller Approximation Formula for the volatility, o, of a Problem 8: stock X -K X -K . -K2 is given by o- vtip C - **/c-XX (=k3 .tx+K TT where K is the present value of the strike price...

URGENTTTTTT!!!! 1) A European call option with a strike price of $55 costs $6.1. A European put option with the same strike price and expiration date costs $4.6. For what range of stock prices would...