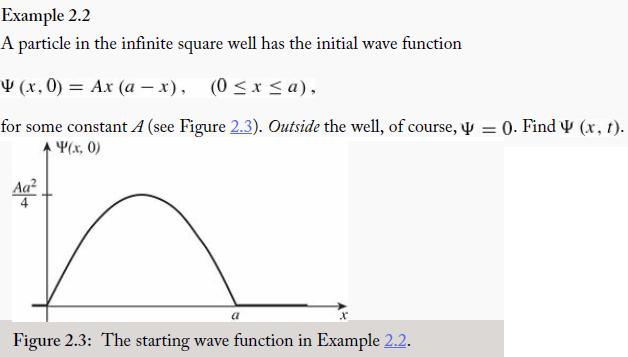
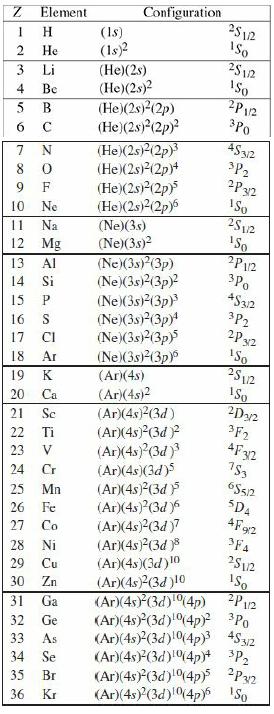
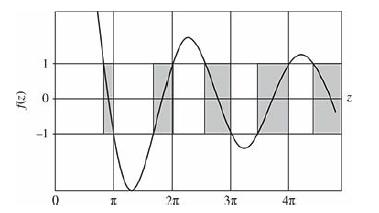
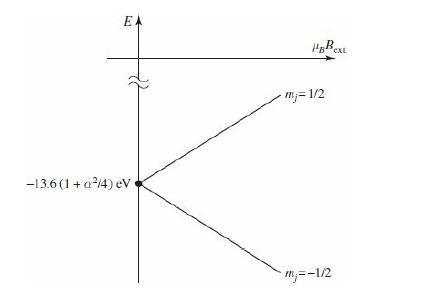
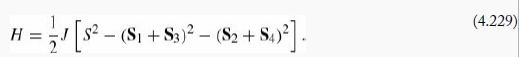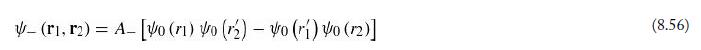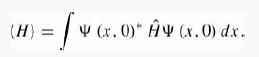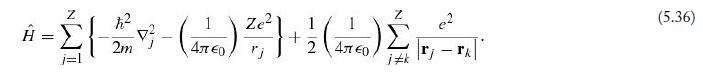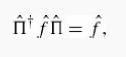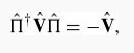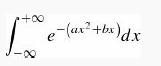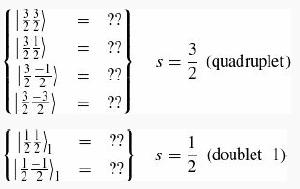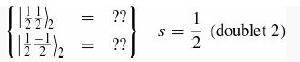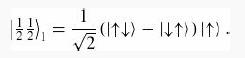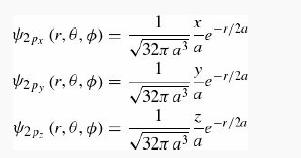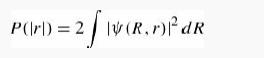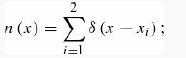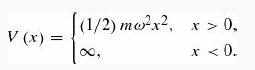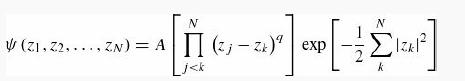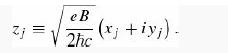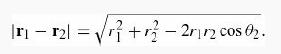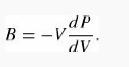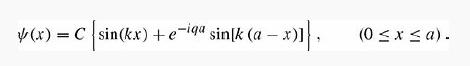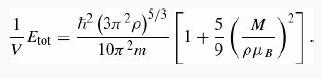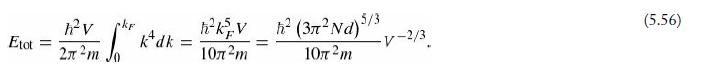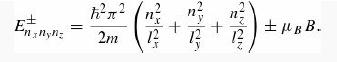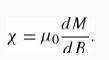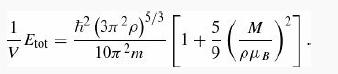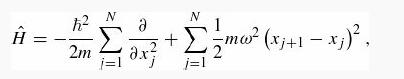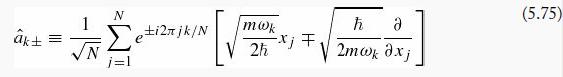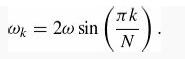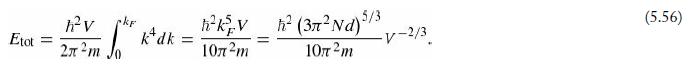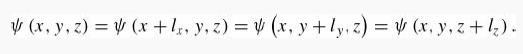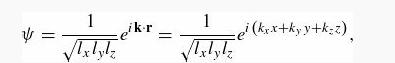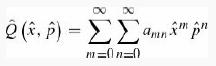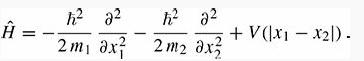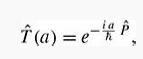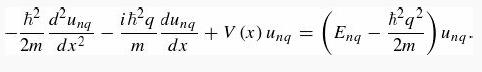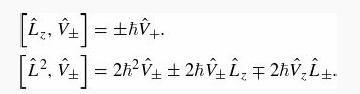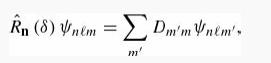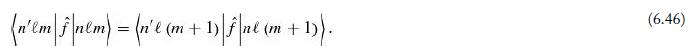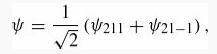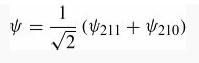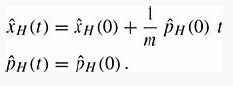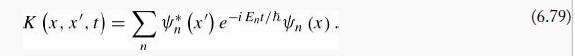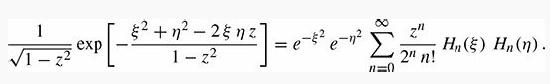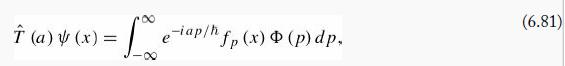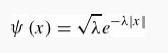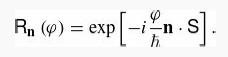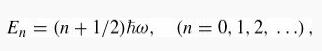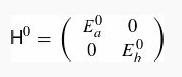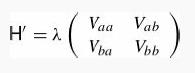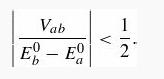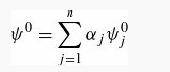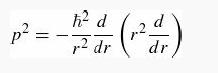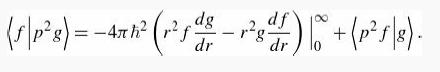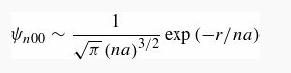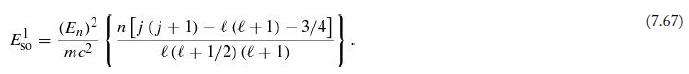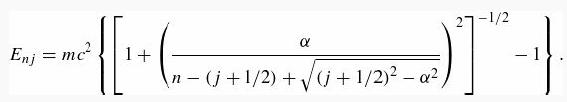Introduction To Quantum Mechanics 3rd Edition David J. Griffiths, Darrell F. Schroeter - Solutions

Discover the ultimate resource for "Introduction To Quantum Mechanics 3rd Edition" by David J. Griffiths and Darrell F. Schroeter. Access comprehensive answers key and solutions manual with solved problems, ensuring your understanding of complex concepts. Dive into chapter solutions and step-by-step answers, perfect for students and instructors alike. Enhance your learning with our test bank and instructor manual, tailored to meet academic needs. Whether you need textbook insights or solutions pdf, explore our free download for reliable assistance. Transform your study sessions with these invaluable questions and answers, providing clarity and confidence in quantum mechanics.