The Dirac delta function can be thought of as the limiting case of a rectangle of area
Question:
The Dirac delta function can be thought of as the limiting case of a rectangle of area 1, as the height goes to infinity and the width goes to zero. Show that the delta-function well (Equation 2.117) is a “weak” potential (even though it is infinitely deep), in the sense that z0 → 0 . Determine the bound state energy for the delta-function potential, by treating it as the limit of a finite square well. Check that your answer is consistent with Equation 2.132. Also show that Equation 2.172 reduces to Equation 2.144 in the appropriate limit.
![]()

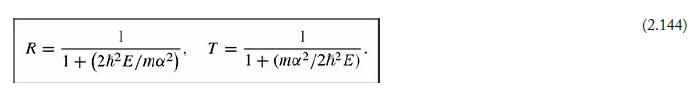

Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Introduction To Quantum Mechanics
ISBN: 9781107189638
3rd Edition
Authors: David J. Griffiths, Darrell F. Schroeter
Question Posted:





