Suppose that \(X\) is a continuous random variable that takes on values in \((0,1)\) and has characteristic function \(\psi(t)=[\exp (i t)-1] / i t\). Use Theorem 2.28 to find the density of \(X\).

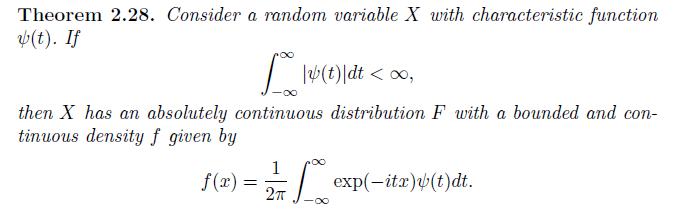
Theorem 2.28. Consider a random variable X with characteristic function (t). If L** \v(t)]dt < , then X has an absolutely continuous distribution F with a bounded and con- tinuous density f given by 1 f(x) = 2 exp(-itx)(t)dt.