A continuous random variable \(Y\) has \(p d f\)

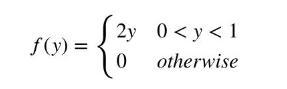
a. Sketch the \(p d f\).

b. Find the \(c d f, F(y)=P(Y \leq y)\) and sketch it. 

c. Use the \(p d f\) and a geometric argument to find the probability \(P(Y \leq 1 / 2)\).

d. Use the \(c d f\) from part (b) to compute \(P(Y \leq 1 / 2)\).

e. Using the \(p d f\) and a geometric argument find the probability \(P(1 / 4 \leq Y \leq 3 / 4)\).

f. Use the \(c d f\) from part (b) to compute \(P(1 / 4 \leq Y \leq 3 / 4)\).

2y f(y) = 0 0 < y < 1 otherwise