Consider the equation

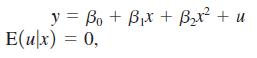
where the explanatory variable x has a standard normal distribution in the population. In particular,

E(x) = 0, E(x²) = Var(x) = 1, and E(x³) = 0. This last condition holds because the standard normal distribution is symmetric about zero. We want to study what we can say about the OLS estimator if we omit x2 and compute the simple regression estimator of the intercept and slope.

(i) Show that we can write

y = α₀ + β₁x + v.

where E(v) = 0. In particular, find v and the new intercept, α₀.

(ii) Show that E1v0x2 depends on x unless β₂ = 0.

(iii) Show that Cov(x, v) = 0.

(iv) If β̂₁ is the slope coefficient from regression yi on xi, is β̂₁ consistent for β₁? Is it unbiased? Explain.

(v) Argue that being able to estimate b1 has some value in the following sense: β₁ is the partial Effect of x on E(y|x) evaluated at x = 0, the average value of x.

(vi) Explain why being able to consistently estimate β₁ and β₂ is more valuable than just estimating b1.

y = Bo + Bix + Bx + u E(ulx) = 0,