Consider the program evaluation problem where w is the binary treatment indicator and the potential outcomes are y(0) and y(1), as we discussed in Sections 3-7e, 4-7, 7-6a, and elsewhere. For a set of control variables x₁, x₂, . . . , x_k, define conditional mean functions for the two counterfactuals:

If y(0) and y(1) are binary, these are the response probabilities. If we wish to move beyond a linear probability model, we would likely use a logit or probit model. If the outcome is a count variable, we would likely use exponential models. We can also use the means from a Tobit if y(0), y(1) are corner solutions.

Recall that the average treatment effect is

(i) Explain why

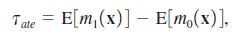
where both expectations are necessarily over the distribution of x.

(ii) If you knew the functions m₀(x) and m₁(x), and you have a random sample

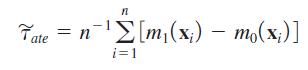
would be an unbiased estimator of τ_ate.

(iii) Now consider the case where we have models, m₀(x, θ₀) and m₁(x, θ₁), where θ₀ and θ₁ are parameters and we have estimators θ̂₀ and θ̂₁. Now how would you estimate τ_ate?

(iv) Define the observed response as usual:

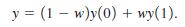
Show that if w is independent of [y(0), y(1)] conditional on x, then

Therefore,

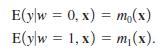
(v) If y(0) and y(1) follow logit or probit models with response probabilities

respectively, how would you estimate all of the parameters? How would you estimate τ_ate?

m,(x) = E[y(0)|x] m,(x) = E[y(1)|x].