Consider the potential outcomes framework, where w is a binary treatment indicator and the potential outcomes are y(0) and y(1). Assume that w is randomly assigned, so that w is independent of [y(0),y(1)]. Let µ₀ = E[y(0)], µ₁ = E[y(1)], s²₀ = Var[y(0)], and s²₁ = Var[y(1)].

(i) Define the observed outcome as y = (1 – w)y(0) + wy(1). Letting τ = µ₁ – µ ₀ be the average treatment effect, show you can write

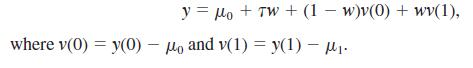
(ii) Let u = (1 – w)v(0) + wv(1) be the error term in

y = µ₀ + τ_w + u

Show that

E(u|w) = 0

What statistical properties does this finding imply about the OLS estimator of t from the simply regression y_i on w_i for a random sample of size n? What happens as n → ∝?

(iii) Show that

Var(u|w) = E(u²|0w) = (1 – w)s²₀ + ws²_1.

Is there generally heteroskedasticity in the error variance?

(iv) If you think s²₁ ¹ s²₀, and τ̂ is the OLS estimator, how would you obtain a valid standard error for τ̂?

(v) After obtaining the OLS residuals, û_i, i = 1, . . . , n, propose a regression that allows consistent estimation of s²₀ and s²₁.

y = lo + TW + (1 w)v(0) + wv(1), where v(0) = y(0) - Mo and v(1) = y(1) H1.