Suppose a short rate process in a risk-neutral world is defined by

\[\mathrm{d} r=\mu(r, t) \mathrm{d} t+\sigma(r, t) \mathrm{d} \hat{z},\]

where \(\hat{z}(t)\) is a standardized Wiener process. A standard way to approximate this equation at a point \((r, t)\) over a small interval \(\Delta t\) is by the binomial tree shown in Figure 16.15. In this approximation,

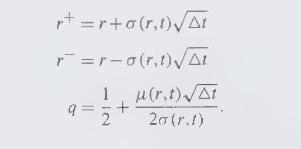
(a) Show that in general this does not produce a recombining lattice. That is, show that an up move followed by a down move is not the same as a down move followed by an up move.

(b) Consider the change of variable

\[w(r, t)=\int_{0}^{r} \frac{\mathrm{d} y}{\sigma(y, t)} .\]

Use Ito's lemma to write the process satisfied by \(w(r, t)\), and show that its volatility term is constant. Conclude that the binomial approximation for \(w(r, t)\) is recombining.

(c) Find the appropriate change of variable for the geometric process \[
\mathrm{d} r=\mu r \mathrm{~d} t+\sigma r \mathrm{~d} \hat{z}
\]

Transcribed Image Text:

+=r+o(r,t) AI r=ra (r,t)At 1 (r,t)t 2 + 20(r.1)