Use the Black-Derman-Toy model with \(b=.01\) to match the term structure of Example 16.7.

Data from Example 16.7

The 12-year term structure has been extended here to 14 years. We will assume that this is the observed spot rate curve. To match it to a full Ho—Lee model, we must make some assumption concerning volatility. Suppose that we have measured the volatility to be .01 per year, which means that the short rate is likely to fluctuate about 1 percentage point during a year.
We can carry out the match using a spreadsheet package that includes an equation-solving routine. The details are shown in Figure 16.11. The first two lines of the figure show the given spot rates over the 14-year period. The next row shows the parameters a, that are used in the Ho—Lee model. These parameters are considered variable by the program. Based on these parameters a short rate lattice is constructed, as shown next in Figure 16.11. From this the forward equations are constructed as another lattice, based on the short rate lattice. The sum of the elements in any column gives the price of a zero-coupon bond with maturity at that date. From these prices, the spot rates can be directly computed. The equation-solving routine is run, adjusting the a,’s until the bottom row matches the assumed spot rate values given in the second row.

Figure 16.11

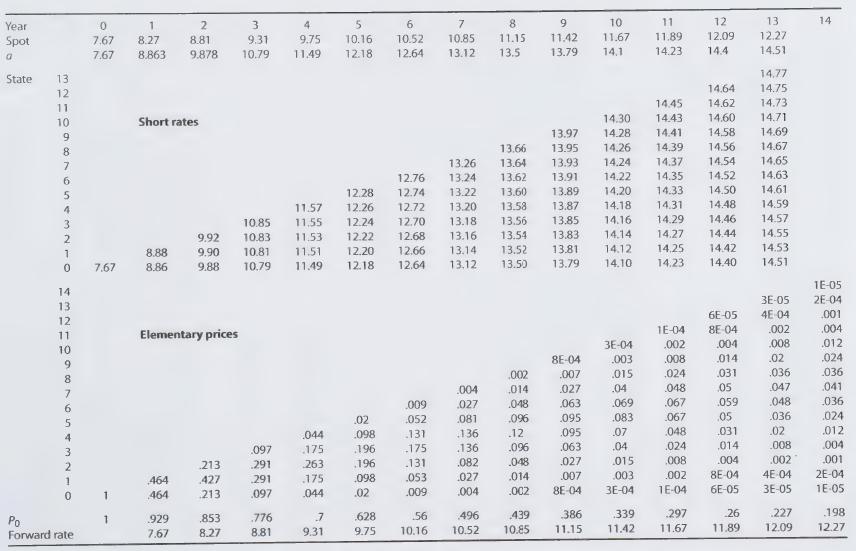
Transcribed Image Text:

Year 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Spot 7.67 8.27 8.81 9.31 9.75 10.16 10.52 10.85 11.15 11.42 11.67 11.89 12.09 12.27 a 7.67 8.863 9.878 10.79 11.49 12.18 12.64 13.12 13.5 13.79 14.1 14.23 14.4 14.51 State 321098965A32TO 14,77 14.64 14.75 11 Short rates 14.45 14.62 14.73 14.30 14.43 14.60 14.71 13.97 14.28 14.41 14.58 14.69 13.66 13.95 14.26 14.39 14.56 14.67 7 13.26 13.64 13.93 14.24 14.37 14.54 14.65 12.76 13.24 13.62 13.91 14.22 14.35 14.52 14.63 12.28 12.74 13.22 13.60 13.89 14.20 14.33 14.50 14.61 11.57 12.26 12.72 13.20 13.58 13.87 14.18 14.31 14.48 14.59 10.85 11.55 12.24 12.70 13.18 13.56 13.85 14.16 14.29 14.46 14.57 9.92 10.83 11.53 12.22 12.68 13.16 13.54 13.83 14.14 14.27 14.44 14.55 8.88 9.90 10.81 11.51 12.20 12.66 13.14 13.52 13.81 14.12 14.25 14.42 14.53 7.67 8.86 9.88 10.79 11.49 12.18 12.64 13.12 13.50 13.79 14.10 14.23 14.40 14.51 1E-05 14 13 12 432 3E-05 2E-04 6E-05 4E-04 .001 11 Elementary prices 10 9 8 1E-04 8E-04 .002 .004 3E-04 .002 .004 .008 .012 8E-04 .003 .008 .014 .02 .024 .002 .007 .015 .024 .031 .036 .036 076543210 .004 .014 .027 .04 .048 .05 047 .041 .009 .027 .048 .063 .069 .067 .059 .048 .036 .02 .052 .081 .096 .095 .083 .067 .05 .036 .024 .044 098 .131 .136 .12 .095 .07 .048 .031 .02 .012 .097 .175 .196 .175 .136 .096 .063 .04 .024 .014 .008 .004 213 .291 263 .196 .131 .082 .048 .027 .015 .008 .004 .0021 .001 464 427 291 .175 .098 .053 .027 014 .007 .003 .002 8E-04 4E-04 2E-04 1 464 213 .097 .044 .02 .009 .004 .002 8E-04 3E-04 1E-04 6E-05 3E-05 1E-05 Po 1 .929 853 .776 7 .628 .56 496 439 .386 .339 .297 .26 .227 198 Forward rate 7.67 8.27 8.81 9.31 9.75 10.16 10.52 10.85 11.15 11.42 11.67 11.89 12.09 12.27