Another solution for Listing 5.9 to find the greatest common divisor of two integers n1 and n2 is as follows: First find d to be the minimum of n1 and n2, then check whether d, d-1, d-2, . . . , 2, or 1 is a divisor for both n1 and n2 in this order. The first such common divisor is the greatest common divisor for n1 and n2. Write a program that prompts the user to enter two positive integers and displays the gcd.

Listing 5.9

Transcribed Image Text:

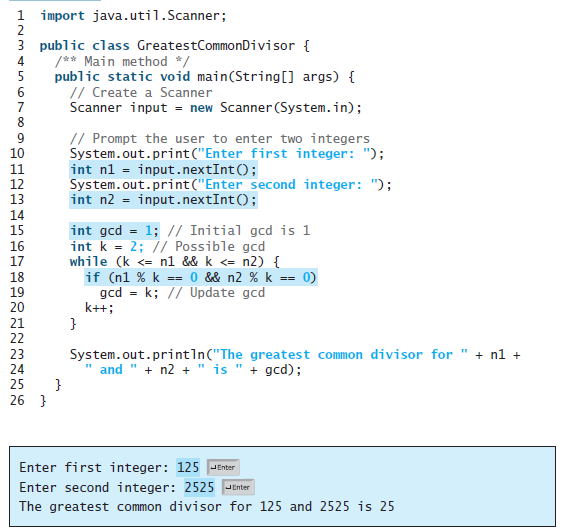
1 import java.util.Scanner; 2 3 public class GreatestCommonDivisor { /** Main method */ public static void main(String[] args) { // Create a Scanner Scanner input = new Scanner (System.in); 5 // Prompt the user to enter two integers System.out.print("Enter first integer: "); int n1 = input.nextInt(); System.out.print("Enter second integer: "); int n2 = input.nextInt(); 10 11 12 13 14 15 int gcd = 1; // Initial gcd is 1 int k = 2; // Possible gcd while (k <= n1 && k <= n2) { if (nl % k == 0 && n2 % k == 0) gcd = k; // Update gcd k++; 16 17 18 19 20 21 22 + n1 + 23 24 25 System.out.println("The greatest common divisor for and " + n2 + " is " + gcd); 26 } Enter first integer: 125 JEnter Enter second integer: 2525 JEnter The greatest common divisor for 125 and 2525 is 25