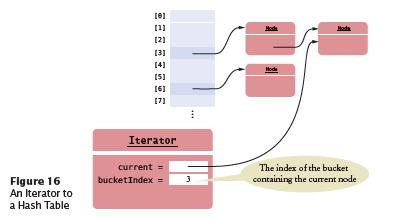
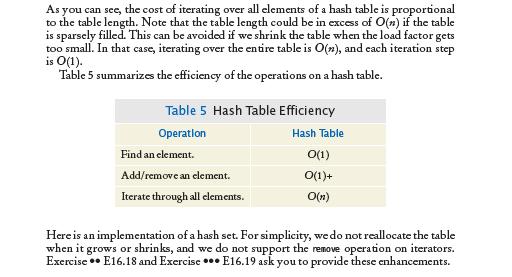
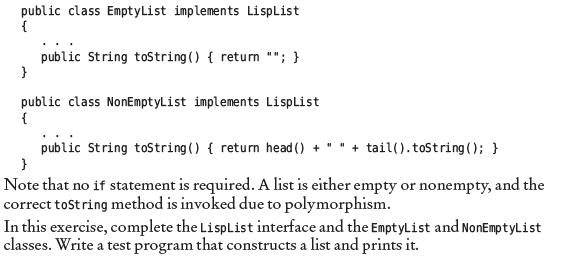
Big Java, Enhanced Early Objects 7th Edition Cay S Horstmann - Solutions

Unlock the full potential of "Big Java, Enhanced Early Objects 7th Edition" by Cay S. Horstmann with our comprehensive resources. Access the complete answers key and explore detailed solutions in our solution manual. Discover step-by-step answers for each chapter, ensuring clarity and understanding. Our collection of solved problems, test bank, and instructor manual provides invaluable support for mastering key concepts. Whether you're looking for textbook solutions or chapter-specific guidance, our platform offers everything you need. Enjoy the convenience of online access and free download options to enhance your learning experience.