Define the Triangle2D class that contains:

■ Three points named p1, p2, and p3 of the type MyPoint with getter and setter methods. MyPoint is defined in Exercise.

Design a class named MyPoint to represent a point with x- and y-coordinates. The class contains:

■ The data fields x and y that represent the coordinates with getter methods.

■ A no-arg constructor that creates a point (0, 0).

■ A constructor that constructs a point with specified coordinates.

■ A method named distance that returns the distance from this point to a specified point of the MyPoint type.

■ A method named distance that returns the distance from this point to another point with specified x- and y-coordinates.

Draw the UML diagram for the class and then implement the class. Write a test program that creates the two points (0, 0) and (10, 30.5) and displays the distance between them.

■ A no-arg constructor that creates a default triangle with the points (0, 0), (1, 1), and (2, 5).

■ A constructor that creates a triangle with the specified points.

■ A method getArea() that returns the area of the triangle.

■ A method getPerimeter() that returns the perimeter of the triangle.

■ A method contains(MyPoint p) that returns true if the specified point p is inside this triangle (see Figure).

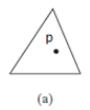
(a) A point is inside the triangle.

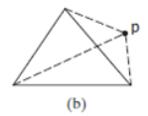
■ A method contains(Triangle2D t) that returns true if the specified triangle is inside this triangle (see Figure).

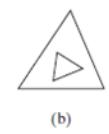
(b) A triangle is inside another triangle.

■ A method overlaps(Triangle2D t) that returns true if the specified triangle overlaps with this triangle (see Figure).

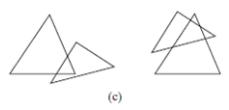
(c) A triangle overlaps another triangle.

Draw the UML diagram for the class and then implement the class. Write a test program that creates a Triangle2D objects t1 using the constructor new Triangle2D(new MyPoint(2.5, 2), new MyPoint(4.2, 3), new MyPoint(5, 3.5)), displays its area and perimeter, and displays the result of t1.contains(3, 3), r1.contains(new Triangle2D(new MyPoint(2.9, 2), new MyPoint(4, 1), MyPoint(1, 3.4))), and t1. overlaps(new Triangle2D(new MyPoint(2, 5.5), new MyPoint(4, -3), MyPoint(2, 6.5))).

(Hint: For the formula to compute the area of a triangle, see Exercise. To detect whether a point is inside a triangle, draw three dashed lines, as shown in Figure. If the point is inside a triangle, each dashed line should intersect a side only once. If a dashed line intersects a side twice, then the point must be outside the triangle. For the algorithm of finding the intersecting point of two lines, see Exercise.)

Write a program that prompts the user to enter three points (x1, y1), (x2, y2), (x3, y3) of a triangle and displays its area. The formula for computing the area of a triangle is

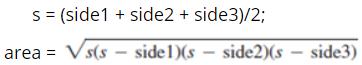
Here is a sample run:

(a) A point is inside the triangle.

(b) A point is outside the triangle.

Two points on line 1 are given as (x1, y1) and (x2, y2) and on line 2 as (x3, y3) and (x4, y4), as shown in Figure. The intersecting point of the two lines can be found by solving the following linear equation:

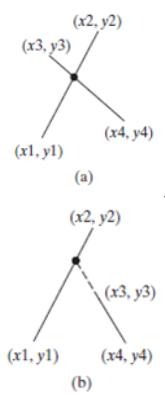
(y1 – y2)x – (x1 – x2)y = (y1 – y2)x1 – (x1 – x2)y1

(y3 – y4)x – (x3 – x4)y = (y3 – y4)x3 – (x3 – x4)y3

This linear equation can be solved using Cramer’s rule (see Exercise). If the equation has no solutions, the two lines are parallel (Figure).

Can the following conversions involving casting be allowed? Write a test program to verify your answer.

A linear equation can be solved using Cramer’s rule given in Exercise. Write a program that prompts the user to enter a, b, c, d, e, and f and displays the result. If ad – bc is 0, report that “The equation has no solution.”

You can use Cramer’s rule to solve the following 2 × 2 system of linear equation:

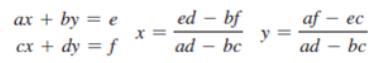
Write a program that solves the following equation and displays the value for x and y:

Write a program that prompts the user to enter four points and displays the intersecting point. Here are sample runs:

Transcribed Image Text:

(a) (b)