Listing 5.15 determines whether a number n is prime by checking whether 2, 3, 4, 5, 6, ..., n/2 is a divisor. If a divisor is found, n is not prime. A more efficient approach is to check whether any of the prime numbers less than or equal to ?n can divide n evenly. If not, n is prime. Rewrite Listing 5.15 to display the first 50 prime numbers using this approach. You need to use an array to store the prime numbers and later use them to check whether they are possible divisors for n.

Listing

Transcribed Image Text:

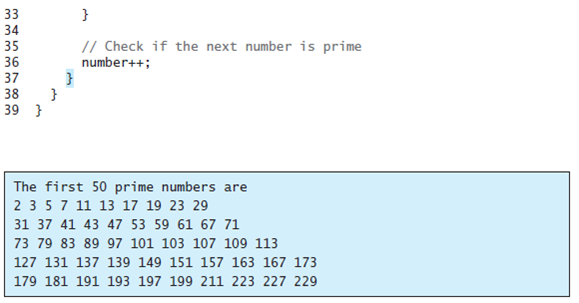
1 public class PrimeNumber { public static void main(String[] args) { final int NUMBER_OF_PRIMES = 50; // Number of primes to display final int NUMBER_OF_PRIMES_PER_LINE = 10; // Display 10 per line 2 3 4. 0; // Count the number of prime numbers 5 int count int number = 2; // A number to be tested for primeness System.out.println("The first 50 prime numbers are \n"); // Repeatedly find prime numbers while (count < NUMBER_OF_PRIMES) { // Assume the number is prime boolean isPrime = true; // Is the current number prime? 10 11 12 13 14 15 16 17 18 19 20 21 // Test whether number is prime for (int divisor = 2; divisor <= number / 2; divisor++) { if (number % divisor == 0) { // If true, number is not prime isPrime = false; // Set isPrime to false break; // Exit the for loop 22 // Display the prime number and increase the count if (isPrime) { count++; // Increase the count 23 24 25 26 27 if (count % NUMBER_OF_PRIMES_PER_LINE == 0) { // Display the number and advance to the new line System.out.println(number); 28 29 30 else System.out.print (number + " "); 31 32 33 34 35 36 37 38 39 } // Check if the next number is prime number++; The first 50 prime numbers are 2 3 57 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229