The problem for finding a largest block is described in Programming Exercise 8.35. Design a dynamic programming algorithm for solving this problem in O(n2) time. Write a test program that displays a 10-by-10 square matrix, as shown in Figure 22.14a. Each element in the matrix is 0 or 1, randomly generated with a click of the Refresh button. Display each number centered in a text field. Use a text field for each entry. Allow the user to change the entry value. Click the Find Largest Block button to find a largest square submatrix that consists of 1s. Highlight the numbers in the block, as shown inFigure 22.14b. See www.cs.armstrong.edu/liang/animation/FindLargestBlock.html? for an interactive test.

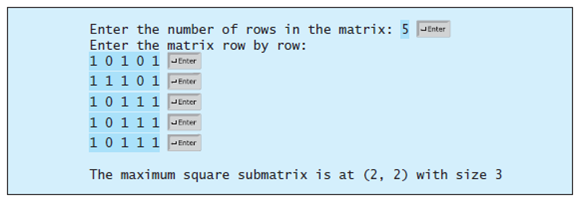
Given a square matrix with the elements 0 or 1, write a program to find a maximum square submatrix whose elements are all 1s. Your program should prompt the user to enter the number of rows in the matrix. The program then displays the location of the first element in the maximum square submatrix and the number of the rows in the submatrix. Here is a sample run:

Your program should implement and use the following method to find the maximum square submatrix:

public static int[] findLargestBlock(int[] [] m)?

The return value is an array that consists of three values. The first two values are the row and column indices for the first element in the submatrix, and the third value is the number of the rows in the submatrix.

1 1 0 1 o o 0 0 1 1 1 1 0 10 1 0 1 10 0 1 1 00 0 0 0 0 0 0 0 0 11 1 o 0 0 10 o 10 1 1 1 1 1 0 1 10 1 1 1 1 0 1 10 1 0 0 0 1 1 1 0 1 o 0 10 0 1 1 0 0 0 0 0 1 0 1 0 0 10 0 1 10 1 1 1 1 0 1 0 1 1 1 101 1 1 1 Refresh Refresh Find Largest Block Find Largest Block (a) (b) 1. 1. 1. 1. 1. 1, 1. 1. 1. Enter the number of rows in the matrix: 5 JEnter Enter the matrix row by row: 10 10 1 Jtnter 11 10 1 -Enter 10 1 11 Jnter 10111 Jenter 10111 - Enter The maximum square submatrix is at (2, 2) with size 3