A rotation on a computer screen is sometimes implemented as the product of two shear-and-scale transformations, which can speed up calculations that determine how a graphic image actually appears in terms of screen pixels. (The screen consists of rows and columns of small dots, called pixels.) The first transformation A₁ shears vertically and then compresses each column of pixels; the second transformation A₂  shears horizontally and then stretches each row of pixels. Let

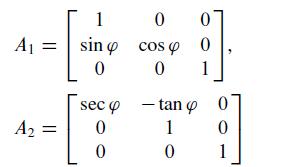
Show that the composition of the two transformations is a rotation in R².

A = A = 1 sin 0 seco 0 0 0 cos 0 0 0 ;]. 1 - tany 1 0 0 1