Another estimate can be made for an eigenvalue when an approximate eigenvector is available. Observe that if Ax = x, then x T AX =

Another estimate can be made for an eigenvalue when an approximate eigenvector is available. Observe that if Ax =  λx, then x^TAX = x^T(λx) = λ(x^Tx), and the Rayleigh quotient

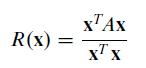
equals λ. If x is close to an eigenvector for λ, then this quotient is close to λ. When A is a symmetric matrix (A^T = A), the Rayleigh quotient R(x_k) = (x^T_k Ax_k)/(x^T_k x_k) will have roughly twice as many digits of accuracy as the scaling factor  μ_k in the power method. Verify this increased accuracy by computing μ_k and R(x_k) for k = 1,...,4.

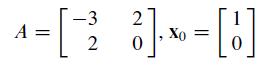
R(x) XTAX XTX