I want to solve them all please

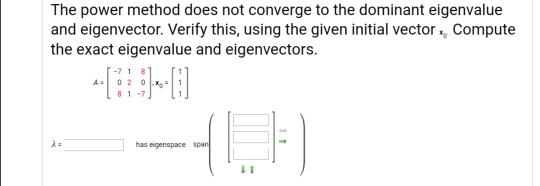
The power method does not converge to the dominant eigenvalue and eigenvector. Verify this, using the given initial vector, Compute the exact eigenvalue and eigenvectors. has eigenspace spa Apply the inverse power method to approximate, for the matrix A, the eigenvalue that is smallest in magnitude. Use the given initial vector Xox iterations, and three-decimal-place accuracy. There is an alternative way to estimate the dominant eigenvalue 11 of matrix A in conjunction with the power method. First, observe that if Ax = 11x, then The expression RX) - (Ax) xxx is called a Rayleigh quotient. As we compute the iterates Xk, the successive Rayleigh quotients R(x) should approach 1,. In fact, for symmetric matrices, the Rayleigh quotient method is about twice as fast as the scaling factor method. To see how the Rayleigh quotient method approximates the dominant eigenvalue more rapidly than the ordinary power method, compute the successive Rayleigh quotients R(x) for i = 1,...,k for the matrix A. (Round your answer to three decimal places.) Rix) Apply the inverse power method to approximate, for the matrix A, the eigenvalue that is smallest in magnitude. Use the given initial vector kykiterations, and three-decimal-place accuracy. The power method does not converge to the dominant eigenvalue and eigenvector. Verify this, using the given initial vector, Compute the exact eigenvalue and eigenvectors. has eigenspace spa Apply the inverse power method to approximate, for the matrix A, the eigenvalue that is smallest in magnitude. Use the given initial vector Xox iterations, and three-decimal-place accuracy. There is an alternative way to estimate the dominant eigenvalue 11 of matrix A in conjunction with the power method. First, observe that if Ax = 11x, then The expression RX) - (Ax) xxx is called a Rayleigh quotient. As we compute the iterates Xk, the successive Rayleigh quotients R(x) should approach 1,. In fact, for symmetric matrices, the Rayleigh quotient method is about twice as fast as the scaling factor method. To see how the Rayleigh quotient method approximates the dominant eigenvalue more rapidly than the ordinary power method, compute the successive Rayleigh quotients R(x) for i = 1,...,k for the matrix A. (Round your answer to three decimal places.) Rix) Apply the inverse power method to approximate, for the matrix A, the eigenvalue that is smallest in magnitude. Use the given initial vector kykiterations, and three-decimal-place accuracy