Question: Concern the polynomial and an n n matrix C p called the companion matrix of p: Let p(t) = a 0 + a 1

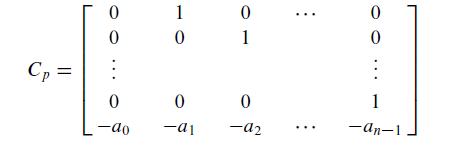
Concern the polynomialp(t)= ao + at +...+ an-1t"-1 +t"and an n × n matrix Cp called the companion matrix of p:image


Let p(t) = a0 + a1t + a2t2 + t3, and let  be a zero of p. 


a. Write the companion matrix for p. 


b. Explain why λ3 = a0 - a1λ - a2λ2, and show that (1, λ, λ2) is an eigenvector of the companion matrix for p.

p(t)= ao + at +...+ an-1t"-1 +t"

Step by Step Solution

★★★★★

3.28 Rating (151 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

a b 0 ... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Linear Algebra And Its Applications Questions!

Q:

240 Payroll Accounting Chapter 7: Comprehensive Projects-Paper-Based Versions One-Month Project NOTE! Templates needed to complete these exercises, including one containing year-to-date payroll data,...

Q:

Let p(f) = a0 + a1f + a2t2 + t3, and let A be a zero of p. a. Write the companion matrix for p. b. Explain why 3 = - a0 - a1 - a22, and show that (1, , 2) is an eigenvector of the companion matrix...

Q:

Let A be a 4 Ã 3 matrix with a2 = a3. If b = a1 + a2 + a3, then the system Ax = b will have infinitely many solutions. In this case answer true if the statement is always true and false...

Q:

Let p() = (-1 )n(n - n-1n-1 -....- 1 - o) he a polynomial of degree n I (a) Show that if i, is a root of p() = 0 then i is an elgenvalue of C with eigenvector x = (in-1,, in-2...... i,1)T , (b) Use...

Q:

Show that there is a change of variables that converts the nth order differential equation x (n) + a n-1 x (n-1) + ....+ a 1 x + a 0 = 0 into a system of n linear differential equations whose...

Q:

Draw pictures to illustrate the case n = 1 and m = 2 of Exercise 8 on page 118 of the Lecture Notes, and explain how your pictures relate to the four hints given there. Question: Exercise 8 on page...

Q:

Consider the time-varying continuous-time system i (t) = A(t)x(t) + B(t)u(t), x(to) = To E Rn (1) where A : R - Rnxn, B : R - R"XP and u : R - RP are continuous functions. Also, denote the transition...

Q:

5. (20 points) Compare two algorithms: Exercise 13, p. 230 (conventional algorithm), and Exercise 14, p. 230 (Horner's method). . A pseudocode for the conventional algorithm for evaluating a...

Q:

An n x n complex matrix A is called skew-hermitian if and only if: A = -A. A real, skew-hermitian matrix is called anti-symmetric or skew-symmetric. a) Let A be a skew-hermitian matrix and suppose A...

Q:

Thanks for you helping! MG7. Let A, / E C and let p(I) be a polynomial of degree n. Show that (D - p . id)(p(x)er) - q(1)ek where D = 4 is the derivative operator and q(r) is a polynomial of degree n...

Q:

Derive the worst case upper bound of the following algorithm. Matrics Multiplication (A, B) { Inxm matrix A II m xp matrix B II n xp matrix C || C=AB Let C be a new matrix of the appropriate size For...

Q:

Harwood Medical Instruments PLC (HMI), based just outside of Birmingham, England, manufactured specialty medical instruments and sold them in market niches that were becoming increasingly competitive...

Q:

Distinguish between the accounting for impairment losses under IFRS and under ASPE. How do IFRS and ASPE account for impairment losses for goodwill?

Q:

Question content area top Part 1 Cash flows used in net present value and internal rate of return analyses ignore _ _ _ _ _ _ _ _ . Question content area bottom Part 1 A . future cost savings B ....

Q:

12. Each individual in a biological population is assumed to give birth at an exponential rate , and to die at an exponential rate . In addition, there is an exponential rate of increase due to...

Q:

The following data show U.S. retail sales of canoes from 1980 through 1997, with data in thousands of boats. a. Construct a graph of the time series. Does the overall trend appear to be upward or...

Q:

The following data describe quarterly residential natural gas sales from 1991 through 1994. Determine the quarterly seasonal indexes, then use these indexes to deseasonalize the original data....

Q:

The National Association of Railroad Passengers has reported the following data describing U.S. commuter train ridership. Year 1995 1996 1997 1998 1999 2000 Riders 42.2 45.9 48.5 54.0 58.3 61.6...

Q:

Gradebook ORION Download Assignment ent Question 4 Presented below are the financial statements of Skysong Company Ltd. SKYSONG COMPANY LTD. Comparative Statements of Financial Position December 31...

Q:

help i am studying (1L) The 2022 accounting records of Bramble Transport provide the following information, BRAMBLE Transport Statement of Cash Flows-Direet Method Cash receipts from cash payments

Q:

On November 1, 2019, Campbell Corporation management decided to discontinue operation of its Rocketeer Division and approved a formal plan to dispose of the division. Campbell is a successful...