Question: Let is an eigenvector for A, and two eigenvalues are .5 and .2. Construct the solution of the dynamical system x k+1 = Ax k

Let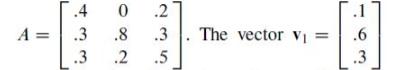 A = .4 .3 .3 0 .8 .2 .2 3. The vector

is an eigenvector for A, and two eigenvalues are .5 and .2. Construct the solution of the dynamical system x_k+1 = Ax_k that satisfies x₀ = (0, .3, .7). What happens to x_k as k → ∞?

A = .4 .3 .3 0 .8 .2 .2 3. The vector V = .5 .1 .6 .3

Step by Step Solution

★★★★★

3.36 Rating (174 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

4 A 3 3 0 2 1 8 3 Given eigenvector V 6 and eigenvalues 5 and 2 To fin... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Linear Algebra And Its Applications Questions!

The following are possible absorption functions. What happens to each as c approaches infinity? Assume that all parameters take on positive values. 1. 2. 3. 4. Ac In(1 +c) e2c c2 1 + 10c

The following differential equations for the production of a chemical P share the properties that the rate of change at t = 0 is 5.0, and the limit as t is 0. For each, find the solution starting...

Solve dx 4d2 + 3y(t) = 2 + x(1) dt for the input x(t) = u(t). The initial conditions are y(0) = 1 and (0) = 2 16

Can you please help me with number 12 and number 15. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! 5.6 Problems Find...

Math 636 Final - Quiz Component 1. The system of linear equations 2x2 x3 = 3 2x1 + x2 + 2x3 = 1 x1 + x2 + 3x3 = 2 (a) is consistent with a unique solution. (b) is consistent with infinitely many...

Can you please help me with number 12 and number 15. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! 5.7 Matrix Exponentials...

Can you please help me with number 31. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! 5.7 Matrix Exponentials and Linear...

Can you please help me with number 21. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! Open with Chapter 5 Linear Systems...

Can you please help me with number 15. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! Linear Systems quations 406 The...

MATHEMATICS FOR MACHINE LEARNING Marc Peter Deisenroth A. Aldo Faisal Cheng Soon Ong Contents Foreword 1 Part I Mathematical Foundations 9 1 Introduction and Motivation 11 1.1 Finding Words for...

1. Nettles' Frame Company constructs two types of picture frames, painted and varnished. Both types of frames are constructed with the same resources, and the daily capacity of those resources can...

Air in a spring loaded piston/cylinder has a pressure that is linear with volume, P = A + BV. With an initial state of P = 150 kPa, V = 1 L and a final state of 800 kPa and volume 1.5 L it is similar...

What is the difference between a savings account and a checking account?

55. Consider a single server queuing system where customers arrive according to a Poisson process with rate , service times are exponential with rate , and customers are served in the order of their...

Is there enough evidence to conclude that there are differences between the three working categories (OCCAT2: 1 = Managerial/professional, 2= Technical/sales/services, 3 = Other) in terms of whether...

Do middle-class households headed by women (HHSEX: 1 = Male, 2 = Female) spend more money on food at home than their male counterparts (FOODHOME)? Conduct a test to answer the question.

Are female and male heads of households equally likely to carry a balance on their credit cards? Conduct a test to determine whether there is a difference between the sexes (HHSEX: 1 = Male, 2 =...

Classified Balance Sheet account titles for retained earnings calculations listed on the Classified Balance Sheet

Perform a horizontal analysis for the balance sheet entry "Accounts Receivable" given below. ( Round to the nearest tenth ) \ table [ [ , , , \ table [ [ Increase / Decrease ] , [ Amount Percent ] ]...

Mr. Aqeel is Account Manager working in Lulu Hypermarket, Ruwi Branch. He was caught many times before due to committing errors in books of accounts like Error of Duplication, Error of Principle,...