(a) Prove that an orthogonal 2 × 2 matrix must have the form

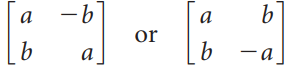
where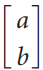

is a unit vector.

(b) Using part (a), show that every orthogonal 2 × 2 matrix is of the form

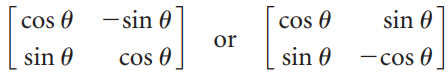
where 0 ‰¤ u ‰¤ 2Ï€.

(c) Show that every orthogonal 2 × 2 matrix corresponds to either a rotation or a reflection in 2.

(d) Show that an orthogonal 2 × 2 matrix Q corresponds to a rotation in R² if det Q = 1 and a reflection in R² if det Q = -1.

or [b -a a b.