(a) Show that the eigenvalues of the 2 × 2 matrix

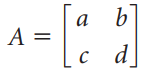
are the solutions of the quadratic equation λ² - tr(A)λ + det A = 0, where tr(A) is the trace of A. (See page 168.)

(b) Show that the eigenvalues of the matrix A in part (a) are

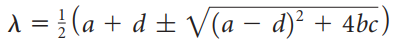
(c) Show that the trace and determinant of the matrix A in part (a) are given by  tr(A) = λ₁ + λ₂ and det A = λ₁λ₂ where λ₁ and λ₂ are the eigenvalues of A.

a A = A = }(a + d V(a d) + 4bc)