Question: In general, it is difficult to show that two matrices are similar. However, if two similar matrices are diagonalizable, the task becomes easier. Show that

In general, it is difficult to show that two matrices are similar. However, if two similar matrices are diagonalizable, the task becomes easier. Show that A and B are similar by showing that they are similar to the same diagonal matrix. Then find an invertible matrix P such that P^-1AP = B.

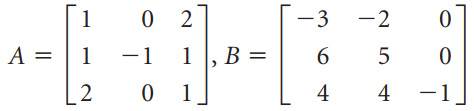
-3 -2 B = 5 -1 -1

Step by Step Solution

★★★★★

3.32 Rating (158 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

So A and B both have eigenvalues 1 and 3 ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Linear Algebra Questions!

Two insulated tanks A and B are connected by a valve. Tank A has a volume of 30 ft3 and initially contains argon at 50 lbf/in 2, 50 F. Tank B has a volume of 60 ft3 and initially contains ethane at...

Two insulated tanks A and B are connected by a valve. Tank A has a volume of 1 m3 and initially contains argon at 300 kPa, 10C. Tank B has a volume of 2 m3 and initially contains ethane at 200 kPa,...

Two closed chambers A and B are connected by a water manometer. If the gage pressure of chamber A is 10 mm of mercury vacuum and the height difference of the water columns is 10 cm: Determine the...

In general, it is difficult to show that two matrices are similar. However, if two similar matrices are diagonalizable, the task becomes easier. In Exercises 1-2 show that A and are similar by...

Consider the following. 1 0 0 A = 5 1 601 List the eigenvalues of A and bases of the corresponding eigenspaces. (Repeated eigenvalues should be entered repeatedly with the same eigenspaces.) O....

In general, it is difficult to show that two matrices are similar. However, if two similar matrices are diagonalizable, the task becomes easier. In the exercise below, show that A and B are similar...

MATHEMATICS FOR MACHINE LEARNING Marc Peter Deisenroth A. Aldo Faisal Cheng Soon Ong Contents Foreword 1 Part I Mathematical Foundations 9 1 Introduction and Motivation 11 1.1 Finding Words for...

Providing Quality School-Based Learning and Support Services 239 Chapter 6 Language and literacy support Your core task The core task of almost all TAs is to support students language and literacy...

Successful College Reading Application of Skills and Strategies Success Strategy 6: Demonstrate Academic Integrity A. Changes in your behaviors, thoughts and perspectives on the use of these...

Educating Managers from an Evidence-Based Perspective Author(s): Denise M. Rousseau and Sharon Mccarthy Source: Academy of Management Learning & Education, Vol. 6, No. 1 (Mar., 2007), pp. 84101...

Caribbean Tours total payroll for the month of January was $600,000. The following withholdings, fringe benefits, and payroll taxes apply: Federal and state income tax withheld ..................

List the four major steps in building decision trees.

On 2 7 - Nov of year 1 , Javier purchased a building, including the land it was on , to assemble his new equipment. The total cost of the purchase was $ 1 , 3 7 9 , 0 0 0 ; $ 3 1 4 , 0 0 0 was...

It is commonly reported that women show more symptoms of anxiety and depression than men. Would the data from Mireaults study support this hypothesis?

Frequently, tests that yield abnormal results are repeated for confirmation. What is the probability that for a normal person a test will be at least 1.5 times as high as the upper limit of normal on...

Suppose that in a pharmacologic study involving 6000 patients, 75 patients have blood-glucose levels at least 1.5 times the upper limit of normal on one occasion. What is the probability that this...

Suppose a change of 0.30 mg/dL in serum levels is proposed as a test criterion for compliance; that is, a patient who shows a change of ¥ 0.30 mg/dL is considered a compliant vitamin E taker. If...

QUESTION 10 According to a Field Poll, 294 out of 511 of California adults feel that "education and our schools" is one of the top issues facing California. We wish to construct a 90% confidence...

3: Problem 5 Previous Problem List Next (1 point) Your grandmother gives you 210 dollars for your birthday, which you invest in a mutual fund on January 1, 2002. On June 1, 2002, she gives you 610...

Fanning Electronics is considering investing in manufacturing equipment expected to cost $250.000. The equipment has an estimated useful life of four years and a salvage value of $ 19,000. It is...