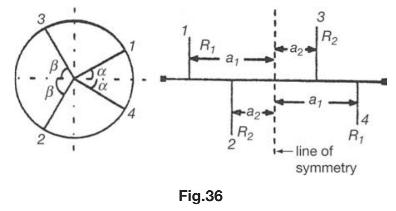
Question: A four-cylinder symmetrical in-line engine is shown in the given Fig.36. Reciprocating weights per cylinder are (R_{1}) and (R_{2}) and the corresponding angular disposition of
A four-cylinder symmetrical in-line engine is shown in the given Fig.36. Reciprocating weights per cylinder are \(R_{1}\) and \(R_{2}\) and the corresponding angular disposition of the crank are \(\alpha\) and \(\beta\) Which one of the following equations should be satisfied for its primary force balance?
(a) \(a_{1} \tan \alpha=a_{2} \tan \beta\)
(b) \(\cos \alpha=\frac{1}{2} \sec \beta\)
(c) \(R_{1} a_{1} \sin 2 \alpha=-R_{2} a_{2} \sin 2 \beta\)
(d) \(R_{1} \cos \alpha=R_{2} \cos \beta\).
2 R R2 a a2 3 a. a2 R R2 2 -line of symmetry Fig.36
Step by Step Solution
3.43 Rating (153 Votes )
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


