In Example 6. 20, we found a bound on the lowest eigenvalue for the given eigenvalue problem.

a. Verify the computation in the example.

b. Apply the method using

\[y(x)=\left\{\begin{array}{cc} x, & 0.\]

Is this an upper bound on \(\lambda_{1}\) ?

c. Use the Rayleigh quotient to obtain a good upper bound for the lowest eigenvalue of the eigenvalue problem: \(\phi^{\prime \prime}+\left(\lambda-x^{2}\right) \phi=0\), \(\phi(0)=0, \phi^{\prime}(1)=0\).

Data from Example 6.20

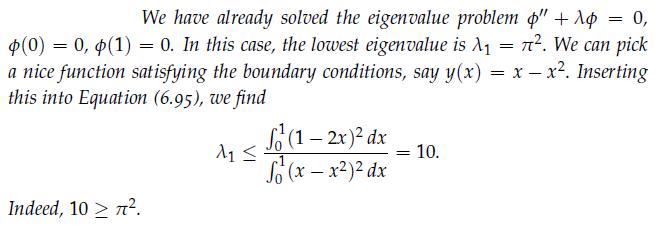
We have already solved the eigenvalue problem " + 1 = 0, $(0) = 0, (1) = 0. In this case, the lowest eigenvalue is A = . We can pick nice function satisfying the boundary conditions, say y(x) = x - x. Inserting this into Equation (6.95), we find (1-2x) dx 1 = 10. So (x-x)2 dx Indeed, 10> .