Empirical evidence reveals that the long rate and the spread (short rate minus long rate) are almost uncorrelated. Suppose we choose the stochastic state variables in the two-factor interest rate model to be the spread s and the long rate ℓ, where

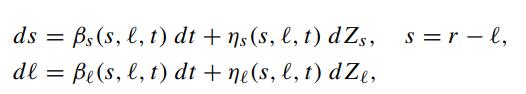
where r is the short rate. Assuming zero correlation between the above processes, show that the price of a default free bond B(s,ℓ,τ) is governed by

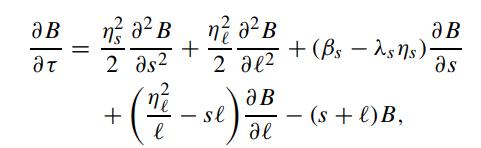
where λ_s is the market price of spread risk and the market price of long rate risk is given by (7.3.14). Schaefer and Schwartz (1984) proposed the following specified stochastic processes for s and ℓ

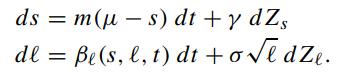
Show that the above bond price equation becomes

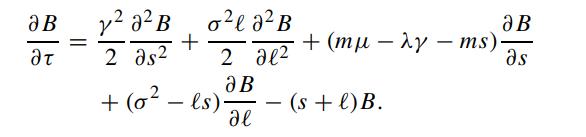The payoff function at maturity is B(s,ℓ,0) = 1. The following analytic approximation procedure is proposed to solve the above equation. They take the coefficient of ∂B/∂ℓ to be constant by treating s as a frozen constant ŝ. Now, we write the bond price as the product of two functions, namely,

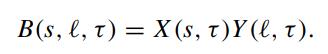
Show that the bond price equation can be split into the following pair of equations: 

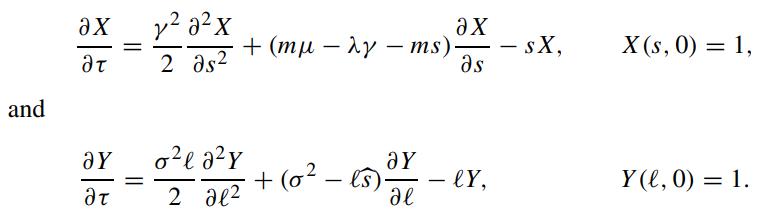
Assuming that all parameters are constant, solve the above two equations for X(s,τ) and Y(ℓ,τ).

Transcribed Image Text:

ds Bs (s, l, t) dt+ns (s, l, t) dZs, = dl= Be(s, l, t) dt + ne(s, l, t) dze, s=r-l,