Show that Note that By considering the Taylor expansion of n(p ln u d ln d) and np (1 p)(ln u d) 2 in powers of t, show that where nt lim (n, k, p') N(d) n where p' ue ueratp and d In (r ) t OT...

To show the given result lets consider the Taylor expansion of the expression np I ...

Show that Note that By considering the Taylor expansion of n(p ln u/d + ln d) and

Question:

Show that

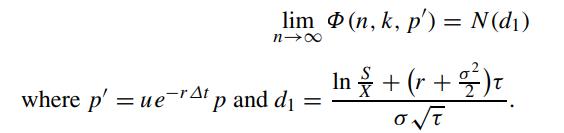
lim (n, k, p') = N(d) n where p'ue ueratp and d = In + (r + ) t OT

Note that

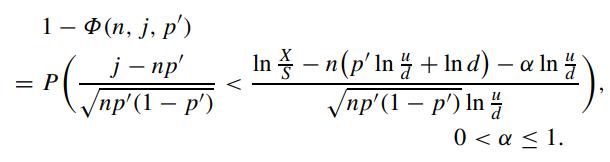
|| 1 - (n, j, p') j - np' ( P p'(1 p') V In-n(p' In + In d) a ln np'(1 - p') In 0 < a < 1.

By considering the Taylor expansion of n(p′ ln u/d + ln d) and np′ (1 − p′)(ln u/d)² in powers of Δt, show that

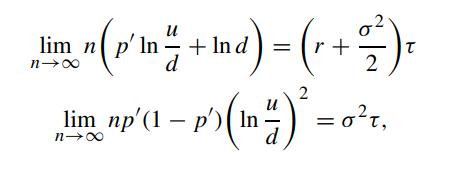
lim n _n (pln = 2 + Ind) = (r + 2/) + T d nx ~195 2 lim_ap(1 p') (n ) = n - In =ot,

where nΔt = τ .

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Mathematical Models Of Financial Derivative

ISBN: 9783642447938

2nd Edition

Authors: Yue-Kuen Kwok

See More Books

Question Posted: Dec 05, 2023 01:13 AM

See More Questions

Suppose we let y = ln S, the KamradRitchken trinomial scheme can be expressed as Show that the Taylor expansion of the above trinomial scheme is given by Given the probability values stated in...
The following additional information is available for the Dr. Ivan and Irene Incisor family from Chapters 1-5. Ivan's grandfather died and left a portfolio of municipal bonds. In 2012, they pay Ivan...
Let b n denote the number of different binary trees with?n?nodes. In this problem, you will find a formula for?b n , as well as an asymptotic estimate. a.?Show that?b 0 =?1?and that, for?n???1, b....
Cover time. Write a program that estimates the time required for the random surfer to visit every page at least once, starting from a random page.
IDENTIFICATION OF OPERATING, INVESTING, AND FINANCING ACTIVITIES The following activities took place in Tomberlin Company during the most recent year. Indicate whether each activity is a cash inflow...
Financial statements for Nackawic Inc. follow: Additional information: 1. Long-term investments were sold for $5,000, resulting in a realized loss of $7,500. 2. New equipment costing $141,000 was...
6. You are valuing an industrial firm whose enterprise value is $10.0 billion. The company has no straight debt but does have 100,000 convertible bonds outstanding. The market value of each bond is...
Jills Job Shop buys two parts (Tegdiws and Widgets) for use in its production system from two different suppliers. The parts are needed throughout the entire 52-week year. Tegdiws are used at a...
On April 1, 2019, Wolf Company borrowed $5,000 on an 8% note payable. The maturity date of the note (and payment of all interest) is July 1, 2020. The accounting period ends December 31. Assume no...
Consider the nodes in the binomial tree employed for the numerical valuation of an American put option on a nondividend paying asset. The (n,j)th node corresponds to the node which is n time steps...
Suppose the underlying asset is paying a continuous dividend yield at the rate q, the two governing equations for u,d and p are modified as Show that the parameter values in the binomial model are...
To add critical observations on the limitations of employee rights in the UK.
Based on contract law principles, do you think the jury\'s verdict against the Loewen Group for $ 5 0 0 million was appropriate? Why or why not? What factors should the jury have considered in...
5.) Consider you have two systems - one filled with (1kg) water and the other with (1kg) of air. Both systems are at 1000 kPa and 30 C. Determine numerically which fluid system has the larger...
Question 3: The partnership of Blossom, Blue, and Kingbird engaged you to adjust its accounting records and convert them uniformly to the accrual basis in anticipation of admitting Kerns as a new...
Instructions : Build an Excel spreadsheet using the accounting equation (Assets = Liabilities + Shareholders' Equity). Remember that each transaction has an equal effect on both the left-hand side...
7.3 Fill in the spreadsheet below to calculate the port- folio return and risk between Zenon and Dynamics, given the 10 years of annual returns for each stock and portfolio weights of 50/50. (a) How...
Suppose that {v1, v2, ( ( ( ( vn} is a linearly independent set of vectors in Rn and let A be a singular matrix. Prove or disprove that {Av1, Av2, ( ( ( ( Avn} is linearly independent.
What did Lennox gain by integrating their WMS, TMS, and labor management systems?
Analyze Instacart using the value chain and competitive forces models. What competitive forces does the company have to deal with? What is its value proposition?
Explain how Instacarts business model works. How does the company generate revenue?
What is the role of information technology in Instacarts business model?
Minden Company introduced a new product last year for which it is trying to find an optimal selling price. Marketing studies suggest that the company can increase sales by 5,000 units for each $2...
Prepare the adjusting journal entries and Post the adjusting journal entries to the T-accounts and adjust the trial balance. Dresser paid the interest due on the Bonds Payable on January 1. Dresser...
Venneman Company produces a product that requires 7 standard pounds per unit. The standard price is $11.50 per pound. If 3,900 units required 28,400 pounds, which were purchased at $10.92 per pound,...

Show that Note that By considering the Taylor expansion of n(p ln u/d + ln d) and

Question:

lim (n, k, p') = N(d₁) n→∞ where p' =ue ueratp and d₁ = In +(r + ²) t O√T

Step by Step Answer:

To show the given result lets consider the Taylor expansion of the expression np I...View the full answer

Mathematical Models Of Financial Derivative

Students also viewed these Business questions