Suppose we define the flexible geometric average G_F (n) of asset prices at n evenly spaced time instants by

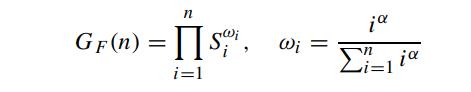and S_i is the asset price at time t_i. Here, ω_i is the weighting factor associated with S_i. Note that the larger the value of α, the heavier are the weights allocated to the more recent asset price. Under the risk neutral measure, the asset price is assumed to follow the Geometric Brownian process

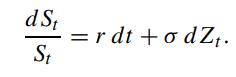
We consider the fixed strike Asian option with terminal payoff 

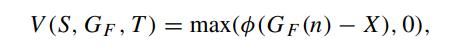
where X is the strike price, and ∅ is the binary variable which is set to 1 for a call or −1 for a put. Show that the Asian option value is given by (Zhang, 1994)

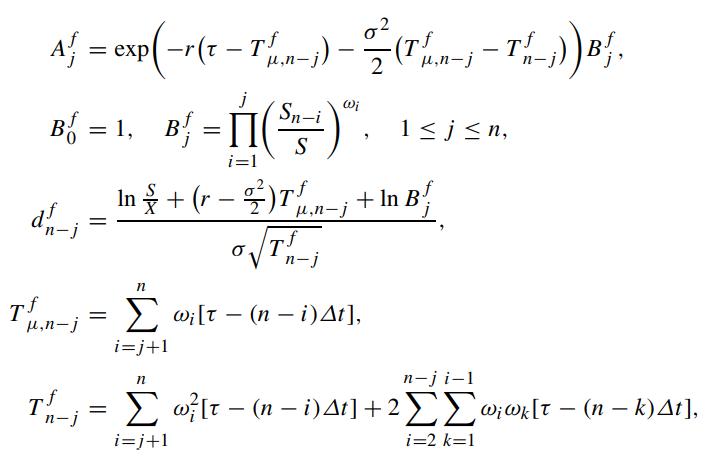
n is the number of asset prices taken for averaging, Δt is the time interval between successive observational instants, j is the number of observations already passed, B^f_j can be considered as the weighted average of the returns of those observations that have already passed.

Transcribed Image Text:

η Gr(n) = Πs, i=1 Wi n i=l