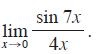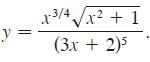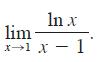![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


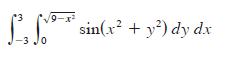
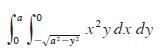
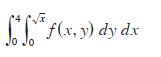
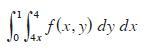
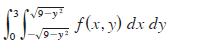
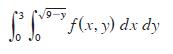
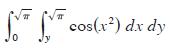
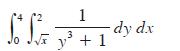
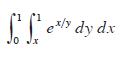
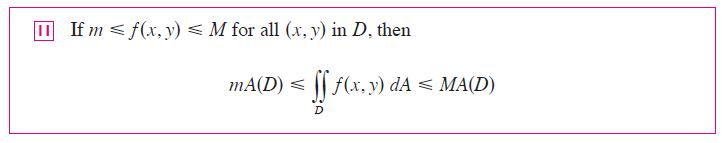

![[*] [0] = y](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1698/2/2/3/8806538d708272d21698223879829.jpg)
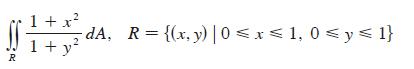
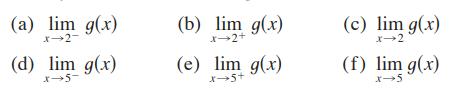
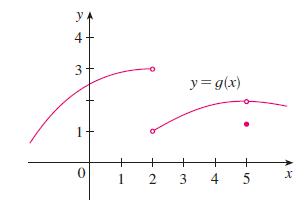
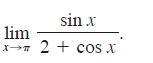
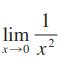
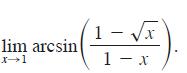
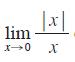
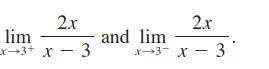
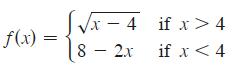
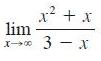
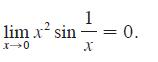
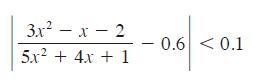

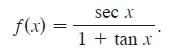
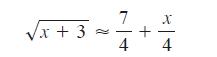
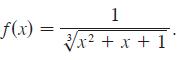
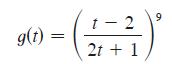
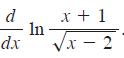
![d dx [tanh (sin .x)].](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1698/7/3/3/51065409dc644d441698733507295.jpg)