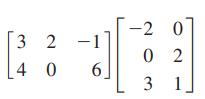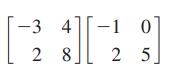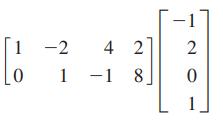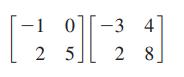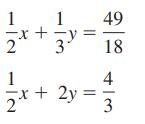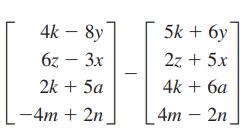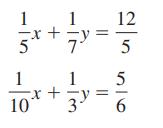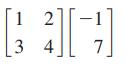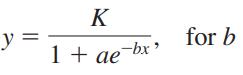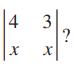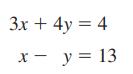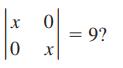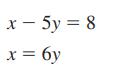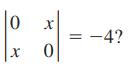Essentials Of College Algebra 12th Edition Margaret Lial, John Hornsby, David Schneider, Callie Daniels - Solutions
Discover the ultimate resource for mastering "Essentials Of College Algebra 12th Edition" by Margaret Lial, John Hornsby, David Schneider, and Callie Daniels. Access a comprehensive solutions manual with step-by-step answers, making algebra easier than ever. Our online platform offers a complete answers key, enabling you to explore chapter solutions and test bank questions. With solved problems readily available, students can enhance their understanding and excel in their coursework. Download the solutions PDF and instructor manual for free, and dive into a world of questions and answers tailored to your textbook needs.
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()