Question: Find the function whose exact differential is d f = cos (x) sin (y) sin (z)dx +sin (x) cos (y) sin (z)dy +sin (x) sin

Find the function whose exact differential is

d f = cos (x) sin (y) sin (z)dx

        +sin (x) cos (y) sin (z)dy

       +sin (x) sin (y) cos (z)dz

and whose value at (0,0,0) is 0. Find the area of the circle of radius a given by ρ = a by doing the double integral

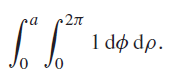
2π οα 1 dφ dρ.

2 1 d d.

Step by Step Solution

★★★★★

3.52 Rating (166 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

Since the differential is exact f x 1 y 1 z 1 f000 ... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Mathematics Physical Chemistry Questions!

Q:

Find the function whose differential is df = cos (x) cos (y)dx sin (x) sin (y)dy and whose value at x = 0, y = 0 is 0.

Q:

In problem find a homogeneous linear differential equation with constant coefficients whose general solution is given. y = c 1 cos x + c 2 sin x + c 3 cos 2x + c 4 sin 2x

Q:

Determine whether the given differential equation is exact. If it is exact, solve it. (sin y - y sin x) dx + (cos x - x cos y - y) dy = 0

Q:

please use this format filename 1 .. 10 name file 2 1 .. 10 1. Find the derivative of f if f (I) = 2-50. Preview will appear here.. Enter math expression here 2. Differentiate the function F(y) =...

Q:

hello need this please exercise 1 Find the partial derivative of the dependent variable with respect to each of the independent variables. z= (7x2 + xy3 ) * dzSolve the given differential equation....

Q:

hello need this test !!! exercise 1 Find the partial derivative of the dependent variable with respect to each of the independent variables. z= (7x2 + xy3 ) * dz\fSolve the given differential...

Q:

buckley (jdb4687) - HW06 - beshaj - (53521) This print-out should have 32 questions. Multiple-choice questions may continue on the next column or page - find all choices before answering. 001 003 2...

Q:

Which of the following expressions is the derivative of y = cos (In (x + 2))? sin (In(r+2)) O A. y= - O B. sin(In(r+2)) = O C. y' = - sin O D. y' = cos 1 sin (In(x+2)) O E. y=Which of the following...

Q:

1. Solve the differential equation 3;! = y3, y(3) = %. 0 None of the other answers is correct 2. Consider the differential equation % = y sin(:r:) with initial condition (7r, 3). First solve this to...

Q:

Evaluating Definite Integrals Use the Substitution Formula in Theorem 7 to evaluate the integrals in Exercises 1-46. 1. a. b. y + 1 dy 2. a. T/4 3. a. tan x sec- x dx b. tan x sec- x dx 4. a. 3 cos x...

Q:

The positron is a particle identical to the electron except that it carries a positive charge of e. Positronium is the bound state of an electron and positron. (a) Calculate the energies of the five...

Q:

Tarzan, who has a mass of 75 kg, holds onto the end of a vine that is at a 13 angle from the vertical. He steps off his branch and, just at the bottom of his swing, he grabs onto his chimp friend...

Q:

Write a function result _ analysis ( labels , predicted ) that takes actual labels from Task 4 and predicted labels from Task 6 and prints the statistical analysis results for your malicious...

Q:

describe the major agencies that facilitate international trade with export insurance and/or loan programmes.

Q:

Suppose there is no real change in the patients underlying mean blood pressure regardless of whether she is on medication. What is the probability that she will be put back on antihypertensive...

Q:

What is the probability that the sample mean will be within 1 unit of the population mean? Suppose we have a population with a normal distribution with mean = 50 and standard deviation = 10. We draw...

Q:

Suppose we want to choose a large enough sample so that the sample mean is within 1 unit of the population mean 99% of the time. What is the minimum sample size to achieve this goal? Suppose we have...

Q:

Calculating the Cost of Equity Smaltz Enterprises is currently involved in its annual review of the firms cost of capital. Historically, the firm has relied on the CAPM to estimate its cost of equity...

Q:

P2-13 (similar to) Question Help Cash flow to owners. Use the data from the following financial statements in the popup window. The comparty paid interest expense of $18,200 for 2017 and had any...

Q:

You run a construction firm. You have just won a contract to build a government office building. It will take one year to construct it requiring an investment of 9.79 million today and 5.0 million in...