A collection of N harmonic oscillators at thermal equilibrium at absolute temperature Tis shown by statistical mechanics to have the thermodynamic energy

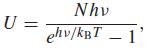
where k_B is Boltzmann’s constant, h is Planck’s constant, T is the absolute temperature, and ν is the vibrational frequency. Find the limit of U as ν → 0. Find the limit of U as T → 0.

As ν → 0, both the numerator and denominator approach zero. We apply l’Hôpital’s rule. The derivative of the numerator with respect to ν is equal to Nh. The derivative of the denominator is

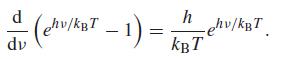
As ν → 0, this derivative approaches h/k_BT.

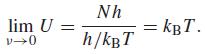
As T → 0 there is no need to apply l’Hôpital’s rule. The numerator remains constant, but the denominator becomes large without bound so that

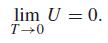
Nhv U = ehv/kBT - 1