Question: If z c (t) is a general solution to the complementary equation and zp(t) is a particular solution to the inhomogeneous equation, show that z

If z_c(t) is a general solution to the complementary equation and zp(t) is a particular solution to the inhomogeneous equation, show that z_c+ z_pis a solution to the inhomogeneous equation of Eq. (12.59).

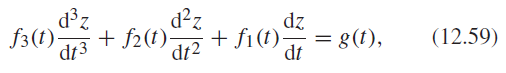
d z + f2(t)- dt3 d?z dz + fi(t) (12.59) = g(t), f3(t)- dt2 dt

Step by Step Solution

★★★★★

3.50 Rating (163 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Since z c satisfies the complem... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Physical Chemistry Questions!

Find the general solution to the system (9.77) for the following matrix pairs: (a) (b) (c) (d) (e) (f) 3 -1 M=(0 3 0 4-2 - 3 2 M= K 2 -1 M= 1200 0 0 6/ -1 3 9 3 -I -1 3 K M= 1311, K= 282 0 1 1

Find the general solution to the following second order systems: (a) (b) (c) (d) d2u dr2 d2v dt 10 0 dr 009) 031 du 6 4 LI Ll

Find the general solution to the following forced second order systems: (a) (b) (c) (d) (e) (f) (g) du 72 dt2 u=(cos t dr3-23 du 136 5 cos 2r cos 2t u:: (lisin 21 cos t Ll sin 2t cos +1-4 6-11-10 dr2...

Question 4 You are given the following nonhomogeneous LDE: d2y E + 4y = 3sin(2x) a) Find the general solution to the complementary equation. [2] b) Also nd the particular solution. (Hint: the most...

Q1: (a) Show that the differential equation is exact. ,_ 3ny2 -2x2y+4 (b) Solve the differential equation. Write your solution in the form F(x,y) = c 3' Find the general solution to the differential...

MATLAB ASSIGN 1- Follow Directions and Complete. Will Thumbs Up! Directions: Unless otherwise specified, your write-up should contain the MATLAB input commands, the corresponding output, and the...

Question 1 1 - Goof: Solve the differential equation 23;" ' + 2y' : Seinfm]. 1. We begin by finding the complementary solution yc = yclim). a. What is the characteristic equation? For this part only....

6. For the differential equation 2 dy+xEy=x (1):3 dx g I a. Make the usual substitution, x = of to restructure this equation as a differential equation with constlant coefficients with respect to the...

A drive has the following parameters: J=10 (kg-m 2 ), T=100-0.1N (N-m), Passive load torque T l =0.05N (N-m), where N is the speed in rpm. Initially the drive is operating in steady-state. Now it is...

Which of the following is true about a firm's average variable cost? It will rise if marginal cost is less than average variable cost. It will never equal the firm's marginal cost. It will decline...

BUSINESSES MAY USE PHYSICAL PROPERTY SUCH A LAND OR A BUILDING OR EQUIPMENT TO SECURE A LOAN. THESE ITEMS WOULD BE CONSIDERED FINANCING ACCOUNTS RECEIVABLE INTEREST COLLATERAL

5 How can you improve your communication with customers and management?

A 1980 study investigated the relationship between the use of OCs and the development of endometrial cancer [9]. The researchers found that of 117 endometrial-cancer patients, 6 had used the OC...

Do these data show a significant association between ethnic origin and genetic type? Ophthalmology Retinitis pigmentosa is a disease that manifests itself via different genetic modes of inheritance....

Compute the Kappa statistic and its standard error regarding reproducibility of the diagnosis of dyspnea in this clinic? Pulmonary Disease One important aspect of medical diagnosis is its...

the following table: (Note: Assume a 365-day year.) a. Calculate the approximate cost of giving up the cash discount from each supplier. a. The approximate cost of giving up the cash discount from...

Route Canal Shipping Company has the following schedule for aging of accounts receivable: a. Calculate the percentage of amount due for each month. b. If the firm had $1,716,000 in credit sales over...

P3-6 (Algo) Analyzing the Effects of Transactions Using T-Accounts, Preparing an Income Statement, and Evaluating the Net Profit Margin Ratio LO3-4, 3-5, 3-6 [The following information applies to the...