Let \(u:[a, b] ightarrow \mathbb{R}\) be a continuous function. Show that \(x \mapsto \int_{[a, x]} u(t) d t\) is everywhere differentiable and find its derivative. What happens if we assume only that \(u \in \mathcal{L}^{1}(d t)\) ? [ consider Theorem 25.20.]

Data from theorem 25.20

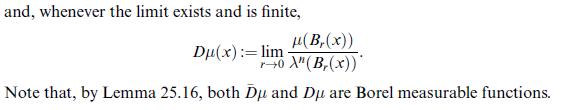
Theorem 25.20 (Lebesgue) Let u L (X"). The limit 1 lim X" (B,(x)) , \u(v) u(x)[X" (dy) =0 B.(x) exists for (Lebesgue) almost all xER". In particular, 1 = lim X" (B(x)) (u(v)X" (dy) a.c. B, u(x) = lim (25.18) (25.19) We will not follow the route laid out above, but use instead the Hardy-Little- wood maximal theorem (Theorem 25.17) to prove Theorem 25.20. The reason is mainly a didactic one, since this is a beautiful example of how weak-type maximal inequalities (i.e. inequalities like (25.14) and (25.11)) can be used to get a.e. convergence. More on this theme can be found in Krantz [26, pp. 27-30] and Garsia [18, pp. 1-4]. Our proof will also show that the limits in (25.18) and (25.19) can be strengthened to B{x}, where B is any ball containing x and, in the limit, shrinking to {x}.