Let \(u \in \mathcal{L}^{2}(\mu)\) be a positive, integrable function. Show that \(\int_{\{u>1\}} u d \mu \leqslant \mu\{u>1\}\) entails that \(u(x) \leqslant 1\) for \(\mu\)-a.e. \(x\).

Remark. This argument is needed for the second part of the proof of Lemma 27.4 (x).

Data from lemma 27.4 (x)

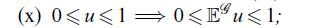
(x) 0